. Econ 551: Lecture Notes
Endogenous Regressors and Instrumental Variables

0. Introduction

These notes introduce students to the problem of endogeneity in linear models and the method of instrumental variables that under certain circumstances allows consistent estimation of the structural coefficients of the endogenous regressors in the linear model. Sections 1 and 2 review the linear model and the method of ordinary least squares (OLS) in the abstract ( ) setting, and the concrete ( ) setting. The abstract setting allows us to define the ``theoretical'' regression coefficient to which the sample OLS estimator converges as the sample size . Section 3 discusses the issue of non-uniqueness of the OLS coefficients if the regressor matrix does not have full rank, and describes some ways to handle this. Seftion 4 reviews the two key asymptotic properties of the OLS estimator, consistency and asymptotic normality. It derives a heteroscedasticity-consistent covariance matrix estimator for the limiting normal asymptotic distribution of the standardized OLS estimator. Section 5 introduces the problem of endogeneity, showing how it can arise in three different contexts. The next three sections demonstrate how the OLS estimator may not converge to the true coefficient values when we assume that the data are generated by some ``true'' underlying structural linear model. Section 6 discusses the problem of omitted variable bias. Section 7 discusses the problem of measurement error. Section 8 discusses the problem of simultaneous equations bias. Section 9 introduces the concept of an instrumental variable and proves the optimality of the two stage least squares (2SLS) estimator.

1. The Linear Model and Ordinary Least Squares (OLS) in : We consider regression first in the abstract setting of the Hilbert space . It is convenient to start with this infinite-dimensional space version of regression, since the least squares estimates can be viewed as the limiting result of doing OLS in , as . In it is more transparent that we can do OLS under very general conditions, without assuming non-stochastic regressors, homoscedasticity, normally distributed errors, or that the true regression function is linear. Regression is simply the process of orthogonal projection of a dependent variable onto the linear subspace space spanned by K random variables . To be concrete, let be a dependent variable and is a vector of explanatory variables. Then as long as and exist and are finite, and as long as is a nonsingular matrix, then we have the identity:

 

where is the least squares estimate given by:

 

Note by construction, the residual term is orthogonal to the regressor vector ,

 

where defines the inner product between two random variables in . The orthogonality condition (3) implies the Pythagorean Theorem

where . From this we define the as

Conceptually, is the cosine of the angle between the vectors and in . The main point here is that the linear model (1) holds ``by construction'', regardless of whether the true relationship between and , the conditional expectation is a linear or nonlinear function of . In fact, the latter is simply the result of projecting into a larger subspace of , the space of all measurable functions of . The second point is that definition of insures the matrix is ``exogenous'' in the sense of equation (3), i.e. the error term is uncorrelated with the regressors . In effect, we define in such a way so the regressors are exogenous by construction. It is instructive to repeat the simple mathematics leading up to this second conclusion. Using the identity (1) and the definition of in (2) we have:

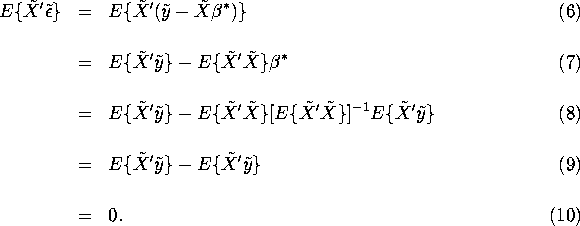
2. The Linear Model and Ordinary Least Squares (OLS) in : Consider regression in the ``concrete'' setting of the Hilbert space . The dimension N is the number of observations, where we assume that these observations are IID realizations of the vector of random variables . Define and , where each is and each is i . Note y is now a vector in . We can represent the matrix X as K vectors in : , where is the column of X, a vector in . Regression is simply the process of orthogonal projection of the dependent variable onto the linear subspace spanned by the K columns of . This gives us the identity:

 

where is the least squares estimate given by:

 

and by construction, the residual vector is orthogonal to the matrix of regressors:

 

where defines the inner product between two random variables in the Hilbert space . The orthogonality condition (13) implies the Pythagorean Theorem

where . From this we define the (uncentered) as

Conceptually, is the cosine of the angle between the vectors y and in .

The main point of these first two sections is that the linear model -- viewed either as a linear relationship between a ``dependent'' random variable and a vector of ``independent'' random variables in as in equation (1), or as a linear relationship between a vector-valued dependent variable y in , and K independent variables making up the columns of the matrix X in equation (11) -- both hold ``by construction''. That is, regardless of whether the true relationship between y and X is linear, under very general conditions the Projection Theorem for Hilbert Spaces guarantees that there exists vectors and such that and equal the orthogonal projections of and y onto the K-dimensional subspace of and spanned by the K variables in and X, respectively. These coefficient vectors a constructed in such a way as to force the error terms and to be orthogonal to and X, respectively. When we speak about the problem of endogeneity, we mean a situation where we believe there is a that there is a ``true linear model'' relating to where the ``true coefficient vector'' is not necessarily equal to the least squares value , i.e. the error is not necessarily orthogonal to . We will provide several examples of how endogeneity can arise after reviewing the asymptotic properties of the OLS estimator.

3. Note on the Uniqueness of the Least Squares Coefficients

The Projection Theorem guarantees that in any Hilbert space H (including the two special cases and discussed above), the projection P(y|X) exists, where P(y|X) is the best linear predictor of an element . More precisely, if where each , then P(y|X) is the element of the smallest closed linear subspace spanned by the elements of X, that is closest to y:

It is easy to show that is a finite-dimensional linear subspace with dimension . The projection theorem tells us that P(y|X) is always uniquely defined, even if it can be represented as different linear combinations of the elements of X. However if X has full rank, the projection P(y|X) will have a unique representation given by

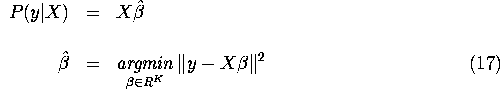
Definition: We say X has full rank, if J = K, i.e. if the dimension of the linear subspace spanned by the elements of X equals the number of elements in X.

It is straightforward to show that X has full rank if and only if the K elements of X are linearly independent, which happens if and only if the matrix X'X is invertible. We use the heuristic notation X'X to denote the matrix whose (i,j) element is . To see the latter claim, suppose X'X is singular. Then there exists a vector such that and , where is the zero vector in . Then we have a'X' Xa = 0 or in inner product notation

However in a Hilbert space, an element has a norm of 0 iff it equals the 0 element in H. Since , we can assume without loss of generality that . Then we can rearrange the equation Xa = 0 and solve for to obtain:

where . Thus, if X'X is not invertible then X can't have full rank, since one of more elements of X are redundant in the sense that they can be exactly predicted by a linear combination of the remaining elements of X. Thus, it is just a matter of convention to eliminate the redundant elements of X to guarantee that it has full rank, which ensures that X'X exists and the least squares coefficient vector is uniquely defined by the standard formula

 

Notice that the above equation applies to arbitrary Hilbert spaces H and is a shorthand for the that solves the following system of linear equations that consistent the normal equations for least squares:

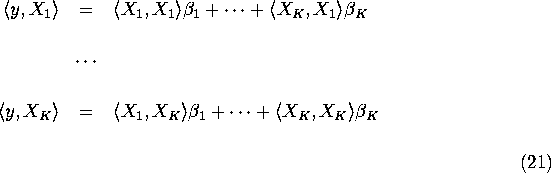
The normal equations follow from the orthogonality conditions , and can be written more compactly in matrix notation as

which is easily seen to be equivalent to the formula in equation (20) when X has full rank and the matrix X'X is invertible.

When X does not have full rank there are multiple solutions to the normal equations, all of which yield the same best prediction, P(y|X). In this case there are several ways to proceed. The most common way is to eliminate the redundant elements of X until the resulting reduced set of regressors has full rank. Alternatively one can compute P(y|X) via stepwise regression by squentially projecting y on , then projecting on and so forth. Finally, one can single out one of the many vectors that solve the normal equations to compute P(y|X). One approach is to use the shortest vector solving the normal equation, and leads to the following formula

 

where is the generalized inverse of the square but non-invertible matrix X'X. The generalized inverse is computed by calculating the Jordan decomposition of [X'X] into a product of an orthonormal matrix W (i.e. a matrix satisfying W'W=WW'=I) and a diagonal matrix D whose diagonal elements are the eigenvalues of [X'X],

Then the generalized inverse is defined by

where is the diagonal matrix whose diagonal element is if the corresponding diagonal element of D is nonzero, and 0 otherwise.

Exercise: Prove that the generalized formula for given in equation (23) does in fact solve the normal equations and results in a valid solution for the best linear predictor . Also, verify that among all solutions to the normal equations, has the smallest norm.

4. Asymptotics of the OLS estimator. The sample OLS estimator can be viewed as the result of applying the ``analogy principle'', i.e. replacing the theoretical expectations in (2) with sample averages in (12). The Strong Law of Large Numbers (SLLN) implies that as we have with probability 1,

The convergence above can be proven to hold uniformly for in compact subsets of . This implies a Uniform Strong Law of Large Numbers (USLLN) that implies the consistency of the OLS estimator (see Rust's lecture notes on ``Proof of the Uniform Law of Large Numbers''). Specifically, assuming is uniquely identified (i.e. that it is the unique minimizer of , a result which holds whenever has full rank as we saw in section 3), then with probability 1 we have

Given that we have a closed-form expression for the OLS estimators in equation (2) and in equation (12), consistency can be established more directly by observing that the SLLN implies that with probability 1 the sample moments

So a direct appeal to Slutsky's Theorem establishes the consistency of the OLS estimator, , with probability 1.

The asymptotic distribution of the normalized OLS estimator, , can be derived by appealing to the Lindeberg-Levy Central Limit Theorem (CLT) for IID random vectors. That is we assume that are IID draws from some joint distribution F(y,X). Since where and

the CLT implies that

 

Then, substituting for in the definition of in equation (12) and rearranging we get:

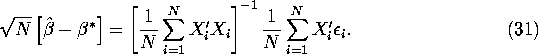
Appealing to the Slutsky Theorem and the CLT result in equation (30), we have:

where the covariance matrix is given by:

In finite samples we can form a consistent estimator of using the heteroscedasticity-consistent covariance matrix estimator given by:

 

where . Actually, there is a somewhat subtle issue in proving that with probability 1. We cannot directly appeal to the SLLN to show that

since the estimated residuals are not IID random variables due to their common dependence on . To establish the result we must appeal to the Uniform Law of Large Numbers to show that uniformly for in a compact subset of we have:

Further more we must appeal to the following uniform convergence lemma:

Lemma: If uniformly with probability 1 for in a compact set, and if with probability 1, then with probability 1 we have:

These results enable us to show that

 

where is a matrix of zeros. Notice that we appealed to the ordinary SLLN to show that the first term on the right hand side of equation (38) converges to and the uniform convergence lemma to show that the remaining two terms converge to .

Finally, note that under the assumption of conditional independence, , and homoscedasticity, , the covariance matrix simplifies to the usual textbook formula:

However since there is no compelling reason to believe the linear model is homoscedastic, it is in general a better idea to play it safe and use the heteroscedasticity-consistent estimator given in equation (34).

5. Structural Models and Endogeneity As we noted above, the OLS parameter vector exists under very weak conditions, and the OLS estimator converges to it. Further, by construction the residuals are orthogonal to X. However there are a number of cases where we believe there is a linear relationship between y and X,

where is not necessarily equal to the OLS vector and the error term is not necessarily orthogonal to X. This situation can occur for at least three different reasons:

1.

Omitted variable bias

2.

Errors in variables

3.

Simultaneous equations bias

We will consider omitted variable bias and errors in variables first since they are the easiest cases to understand how endogeneity problems arise. Then in the next section we will consider the simultaneous equations problem in more detail.

6. Omitted Variable Bias

Suppose that the true model is linear, but that we don't observe a subset of variables which are known to affect y. Thus, the ``true'' regression function can be written as:

where is and is , and and . Now if we don't observe , the OLS estimator based on N observations of the random variables converges to

 

However we have:

 

since for the ``true regression model'' when both and are included. Substituting equation (43) into equation (42) we obtain:

 

We can see from this equation that the OLS estimator will generally not converge to the true parameter vector when there are omitted variables, except in the case where either or where , i.e. where the omitted variables are orthogonal to the observed included variables . Now consider the ``auxiliary regression between and :

 

where is a matrix of regression coefficients, i.e. equation (45) denotes a system of regressions written in compact matrix notation. Note that by construction we have . Substituting equation (45) into equation (44) and simplifying, we obtain:

 

In the special case where , we can characterize the omitted variable bias as follows:

1.

The asymptotic bias is 0 if or , i.e. if doesn't enter the regression equation ( ), or if is orthogonal to ( ). In either case, the restricted regression where is a valid regression and is a consistent estimator of .

2.

The asymptotic bias is positive if and , or if and . In this case, OLS converges to a distorted parameter which overestimates in order to ``soak up'' the part of the unobserved variable that is correlated with .

3.

The asymptotic bias is negative if and , or if and . In this case, OLS converges to a distorted parameter which underestimates in order to ``soak up'' the part of the unobserved variable that is correlated with .

Note that in cases 2. and 3., the OLS estimator converges to a biased limit to ensure that the error term is orthogonal to .

Exercise: Using the above equations, show that .

Now consider how a regression that includes both and automatically ``adjusts'' to converge to the true parameter vectors and . Note that the normal equations when we have both and are given by:

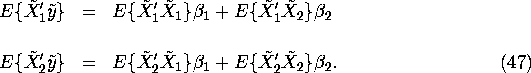
Solving the first normal equation for we obtain:

Thus, the full OLS estimator for equals the biased OLS estimator that omits , , less a ``correction term'' that exactly offsets the asymptotic omitted variable bias of OLS derived above.

Now, substituting the equation for into the second normal equation and solving for we obtain:

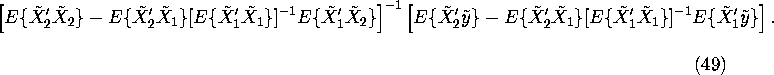
The above formula has a more intuitive interpretation: can be obtained by regressing on , where is the residual from the regression of on :

This is just the result of the second step of stepwise regression where the first step regresses on , and the second step regresses the residuals on , where denotes the projection of on , i.e. where is given in equation (46) above. It is easy to see why this formula is correct. Take the original regression

 

and project both sides on . This gives us

 

since due to the orthogonality condition . Subtracting equation (52) from the regression equation (51), we get

This is a valid regression since is orthogonal to and to and hence it must be orthogonal to the linear combination .

7. Errors in Variables

Endogeneity problems can also arise when there are errors in variables. Consider the regression model

 

where and the stars denote the true values of the underlying variables. Suppose that we do not observe but instead we observe noisy versions of these variables given by:

where , , and . That is, we assume that the measurement error is unbiased and uncorrelated with the disturbances in the regression equation, and the measurement errors in and are uncorrelated. Now the regression we actually do is based on the noisy observed values (y,x) instead of the underlying true values . Substituting for and in the regression equation (54), we obtain:

 

Now observe that the mismeasured regression equation (56) has a composite error term that is not orthogonal to the mismeasured independent variable x. To see this, note that the above assumptions imply that

This negative covariance between x and implies that the OLS estimator of is asymptotically downward biased when there are errors in variables in the independent variable . Indeed we have:

Now consider the possibility of identifying by the method of moments. We can consistently estimate the three moments , and using the observed noisy measures (y,x). However we have

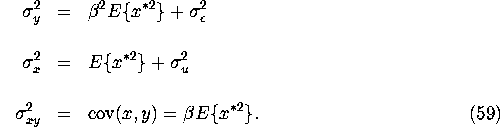
Unfortunately we have 3 equations in 4 unknowns, . If we try to use higher moments of (y,x) to identify , we find that we always have more unknowns that equations.

8. Simultaneous Equations Bias

Consider the simple supply/demand example from chapter 16 of Greene. We have:

 

where y denotes income, p denotes price, and we assume that . Solving we can write the reduced-form which expresses the endogenous variables (p,q) in terms of the exogenous variable y:

 

By the assumption that y is exogenous in the structural equations (60), it follows that the two linear equations in the reduced form, (61), are valid regression equations; i.e. . However p is not an exogenous regressor in either the supply or demand equations in (60) since

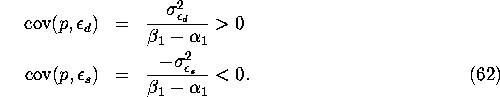
Thus, the endogeneity of p means that OLS estimation of the demand equation (i.e. a regression of q on p and y) will result in an overestimated (upward biased) price coefficient. We would expect that OLS estimation of the supply equation (i.e. a regression of q on p only) will result in an underestimated (downward biased) price coefficient, however it is not possible to sign the bias in general.

Exercise: Show that the OLS estimate of converges to

where

Since , it follows from the above result that OLS estimator is upward biased. It is possible that when is sufficiently small and is sufficiently large that the OLS estimate will converge to a positive value, i.e. it would lead us to incorrectly infer that the demand equation slopes upwards (Giffen good?) instead of down.

Exercise: Derive the probability limit for the OLS estimator of in the supply equation (i.e. a regression of q on p only). Show by example that this probability limit can be either higher or lower than .

Exercise: Show that we can identify from the reduced-form coefficients . Which other structural coefficients are identified?

9. Instrumental Variables We have provided three examples where we are interested in estimating the coefficients of a linear ``structural'' model, but where OLS estimates will produce misleading estimates due to a failure of the orthogonality condition in the linear structural relationship

 

where is the ``true'' vector of structural coefficients. If is endogenous, then , then , and the OLS estimator of the structural coefficients in equation (65) will be inconsistent. Is it possible to consistently estimate when is endogenous? In this section we will show that the answer is yes provided we have access to a sufficient number of instrumental variables.

Definition: Given a linear structural relationship (65), we say the vector of regressors is endogenous if , where , and is the ``true'' structural coefficient vector.

Now suppose we have access to a vector of instruments, i.e. a random vector satisfying:

 

9.1 The exactly indentified case and the simple IV estimator. Consider first the exactly identified case where J = K, i.e. we have just as many instruments as endogenous regressors in the structural equation (65). Multiply both sides of the structural equation (65) by and take expectations. Using A2) we obtain:

 

If we assume that the matrix is invertible, we can solve the above equation for the vector :

 

However plugging in from equation (67) we obtain:

The fact that motivates the definition of the simple IV estimator as the sample analog of in equation (68). Thus, suppose we have a random sample consisting of N IID observations of the random vectors , i.e. our data set consists of which can be represented in matrix form by the vector y, and the matrices Z and X.

Definition: Assume that the matrix Z'X exists. Then the simple IV estimator is the sample analog of given by:

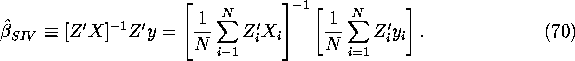
Similar to the OLS estimator, we can appeal to the SLLN and Slutsky's Theorem to show that with probability 1 we have:

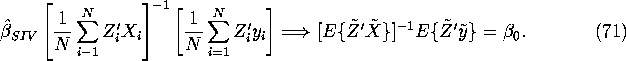
We can appeal to the CLT to show that

where

where we use the result that for any invertible matrix A. The covariance matrix can be consistently estimated by its sample analog:

 

where . We can show that the estimator (74) is consistent using the same argument we used to establish the consistency of the heteroscedasticity-consistent covariance matrix estimator (34) in the OLS case. Finally, consider the form of in the homoscedastic case.

Definition: We say the error terms in the structural model in equation (65) are homoscedastic if there exists a nonnegative constant for which:

A sufficient condition for homoscedasticity to hold is and . Under homoscedasticity the asymptotic covariance matrix for the simple IV estimator becomes:

and if the above two sufficient conditions hold, it can be consistently estimated by its sample analog:

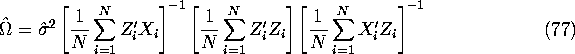
where is consistently estimated by:

 

As in the case of OLS, we recommend using the heteroscedasticity consistent covariance matrix estimator (74) which will be consistent regardless of whether the true model (65) is homoscedastic or heteroscedastic rather than the estimator (78) which will be inconsistent if the true model is heteroscedastic.

9.2 The overidentified case and two stage least squares. Now consider the overidentified case, i.e. when we have more instruments than endogenous regressors, i.e. when J > K. Then the matrix is not square, and the simple IV estimator is not defined. However we can always choose a subset consisting of a subvector of the random vector Z so that is square and invertible. More generally we could construct instruments by taking linear combinations of the full list of instrumental variables , where is a matrix.

 

Example 1. Suppose we want our instrument vector to consist of the first K components of . Then we set where the I is a identity matrix and 0 is a matrix of zeros, and | denotes the horizontal concatenation operator.

Example 2. Consider the instruments given by where . It is straightforward to verify that this is a matrix. We can interpret as the matrix of regression coefficents from regressing on . Thus is the projection of the endogenous variables onto the instruments . Since is a vector of random variables, actually represents the horizontal concatenation of K separate regression coefficient vectors. We can write all the regressions compactly in vector form as

 

where is vector of error terms for each of the K regression equations. Thus, by definition of least squares, each component of must be orthogonal to the regressors , i.e.

 

where is a matrix of zeros. We will shortly formalize the sense in which are the ``optimal instruments'' within the class of instruments formed from linear combinations of in equation (79). Intuitively, the optimal instruments should be the best linear predictors of the endogenous regressors , and clearly, the instruments from the first stage regression (80) are the best linear predictors of the endogenous variables.

Definition: Assume that exists where . Then we define by

 

Definition: Assume that exists where and . Then we define by

 

Clearly is a special case of when . We refer to it as two stage least squares since can be computed in two stages:

Stage 1: Regress the endogenous variables on the instruments to get the linear projections as in equation (80).

Stage 2: Regress on instead of on as shown in equation (83). The projections essentially ``strip off'' the endogenous components of , resulting in a valid regression equation for .

We can get some more intuition into the latter statement by rewriting the original structural equation (65) as:

 

where . Notice that as a consequence of equations (66) and (81). It follows from the projection theorem that equation (84) is a valid regression, i.e. that . Alternatively, we can simply use the same straightforward reasoning as we did for , substituting equation (65) for and simplifying equations (82) and (83) to see that . This motivates the definitions of and as the sample analogs of and :

Definition: Assume where Z is and is , and W'X is invertible (this implies that ). Then the instrumental variables estimator is the sample analog of defined in equation (82):

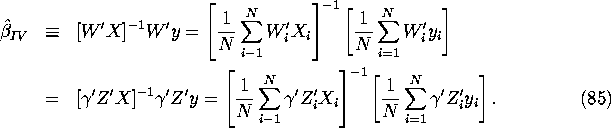
Definition: Assume that the matrix Z'Z and the matrix W'W are invertible, where and . The two-stage least squares estimator is the sample analog of defined in equation (83):

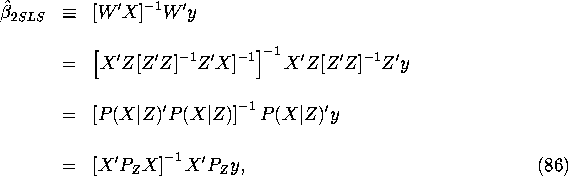
where is the projection matrix

Using exactly the same arguments that we used to prove the consistency and asymptotic normality of the simple IV estimator, it is straightforward to show that and , where is the matrix given by:

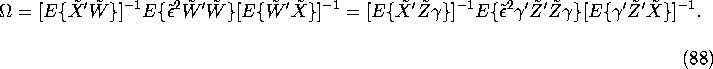
Now we have a whole family of IV estimators depending on how we choose the matrix . What is the optimal choice for ? As we suggested earlier, the optimal choice should be since this results in a linear combination of instruments that is the best linear predictor of the endogenous regressors .

Theorem: Assume that the error term in the structural model (65) is homoscedastic. Then the optimal IV estimator is 2SLS, i.e. it has the smallest asymptotic covariance matrix among all IV estimators.

Proof: Under homoscedasticity, the asymptotic covariance matrix for the IV estimator is equal to

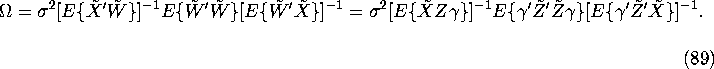
We now show this covariance matrix is minimized when , i.e. we show that

where is the asymptotic covariance matrix for 2SLS which is obtained by substituting into the formula above. Since if and only , it is sufficient to show that , or

Note that and , so our task reduces to showing that

However since fopr some matrix , it follows that the elements of must span a subspace of the linear subspace spanned by the elements of . Then the law of Iterated Projections implies that

This implies that there exists a vector of error terms satisfying

 

where satisfy the orthogonality relation

where is an matrix of zeros. Then using the identity (94) we have

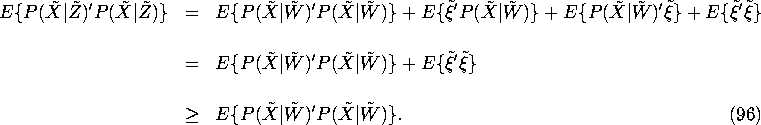
We conclude that , and hence , i.e. 2SLS has the smallest asymptotic covariance matrix among all IV estimators.

There is an alternative algebraic proof that . Given a square symmetric positive semidefinite matrix A with Jordan decomposition A=W D W' (where W is an orthonormal matrix and D is a diagonal matrix with diagonal elements equal to the eigenvalues of A) we can define its square root as

where is a diagonal matrix whose diagonal elements equal the square roots of the diagonal elements of D. It is easy to verify that . Similarly if A is invertible we define as the matrix where is a diagonal matrix whos diagonal elements are the inverses of the square roots of the diagonal element of D. It is easy to verify that . Using these facts about matrix square roots, we can write

 

where M is the matrix given by

It is straightforward to verify that M is idempotent, which implies that the right hand side of equation (98) is positive semidefinite.

It follows that in terms of the asymptotics it is always better to use all available instruments . However the chapter in Davidson and MacKinnon shows that in terms of the finite sample performance of the IV estimator, using more instruments may not always be a good thing. It is easy to see that when the number of instruments J gets sufficient large, the IV estimator converges to the OLS estimator.

Exercise: Show that when J = N and the columns of Z are linearly independent that .

Exercise: Show that when J = K and the columns of Z are linearly independent that .

However there is a tension here, since using fewer instruments worsens the finite sample properties of the 2SLS estimator. A result due to Kinal Econometrica 1980 shows that the moment of the 2SLS estimator exists if and only if

Thus, if J=K 2SLS (which coincides with the SIV estimator by the exercise above) will not even have a finite mean. If we would like the 2SLS estimator to have a finite mean and variance we should have at least 2 more instruments than endogenous regressors. See section 7.5 of Davidson and MacKinnon for further discussion and monte carlo evidence.

Exercise: Assume that the errors are homoscedastic. Is it the case that in finite samples that the 2SLS estimator dominates the IV estimator in terms of the size of its estimated covariance matrix?

Hint: Note that under homoscedasticity, the inverse of the sample analog estimators of the covariance matrix for and are is given by:

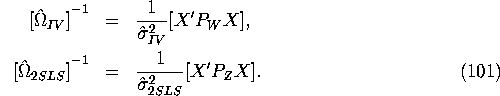
If we assume that , then the relative finite sample covariance matrices for IV and 2SLS depend on the difference

Show that if for some matrix that and this implies that the difference is idempotent.

Now consider a structural equation of the form

 

where the random vector is known to be exogenous (i.e. ), but the random vector is suspected of being endogenous. It follows that can serve as instrumental variables for the variables.

Exercise: Is it possible to identify the coefficients using only as instrumental variables? If not, show why.

The answer to the exercise is clearly no: for example 2SLS based on alone will result in a first stage regression that is a linear function of , so the second stage of 2SLS would encounter multicollinearity. This shows that in order to identify we need additional instruments W that are excluded from the structural equation (103). This results in a full instrument list of size . The discussion above suggest that in order to identity we need and , otherwise we have a multicollinearity problem in the second stage. In summary, to do instrumental variables we need instruments Z which are:

1.

Uncorrelated with the error term in the structural equation (103),

2.

Correlated with the included endogenous variables ,

3.

Contain components which are excluded from the structural equation (103).

• About this document ...