Solutions to Problem Set 1

Economics 551, Yale University

Professor John Rust

Question 1 The choice probability for the general case when

where

The choice probability is given by:

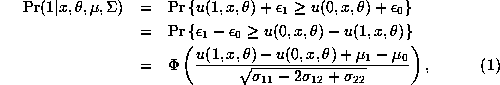
where we use the fact that , so we standardized by subtracting from both sides of the inequality in the probability in the second line of the above equation and divided both sides by its standard deviation, allowing us to use the standard normal CDF in the last line. Note that when and and , this equation reduces to

We note that we must make identifying normalizations of the and parameters of this model, since there are infinitely many different combinations of the 5 free parameters in and that yield the same conditional probability in equation (1), and are thus observationally equivalent. For example, let and let , and be any parameters satisfying 1) is positive semidefinite, and 2) (one example is and ). This model has the same choice probability as the model in equation (2) where , and and . Therefore we need to impose arbitrary identifying normalizations in order to estimate the model. One common normalization is that and and . An alternative identifying normalization is and and a free parameter to be estimated. However whether it is possible to identify the covariance term depends on the specification of the utilities , i=0,1. We will generally need to impose additional identifying normalizations to estimate the parameters of the utilities, , i=0,1. For example if the utility function is linear in parameters, i.e. , i=0,1 with , then it is easy to see that without further restrictions it is not possible to identify and simultaneously, even with the normalization that . To see this, note that for the linear in parameters specification we have:

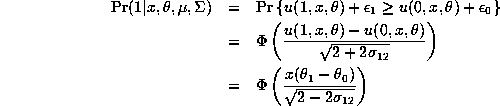
It should be clear that any combination of such that

for a fixed vector are observationally equivalent, and that there are infinitely many such combinations. Therefore we must make a further normalization of the coefficients. A typical normalization is that and that one of the components of is normalized to 1. Since we are free to choose different normalizations, when interpreting the estimation results from the probit model we need to keep the underlying normalization in mind. For the rest of this problem set we will use the normalization and , and . Under this normalization the choice probability is given by , so the estimated value of is interpreted as the impact of an additional unit of x on the incremental utility of choosing alternative 1, i.e.

Question 2 See answers to question 7 and 8 of 1997 Econ 551 problem set 3.

Question 3 The ``true model'' used to generate the data in model 3 was a probit model. Table 1 below presents the true coefficients and the logit and probit estimates of these values which were estimated using the shell program estimate.gpr using two procedures, log_mle.g and prb_mle.g that compute the log-likelihood, gradients and hessians for the logit and probit specifications, respectively. Both log-likelihoods have the following general form:

Notice that the logit parameter estimates are ``further'' from the true parameters than the probit estimates. One ``metric'' for measuring this distance is the Wald test statistic of the hypothesis that the estimated logit parameters equals the true parameters

where is the estimated misspecification-consistent covariance matrix for :

where and are the sample analogs of the hessian and information matrix of the log-likelihood, respectively. Computing the Wald statistic for the misspecified logit model we have , which corresponds to a marginal significance level of given that under the null hypothesis , a Chi-squared random variable with 4 degrees of freedom. The Wald test statistic that the estimated probit parameters equals the true values is , which corresponds to a marginal significance level of 0.594. Thus we can clearly reject the hypothesis that the logit model is correctly specified, but we do not reject the hypothesis that the probit model is correctly specified. However our ability to compute this statistic requires prior knowledge the true parameters . Of course in nearly all ``real'' applications we do not know so this type of Wald test is infeasible.

Later in Econ 551 we will consider general specification tests, such as White's (1982) Econometrica Information matrix test statistic (which is not necessarily a consistent test), or Bieren's (1990) Econometrica specification test statistic of functional form (which is a consistent test). These allow us to test whether the parametric model is correctly specified (i.e. whether there exists a such that , where is the true conditional choice probability) without any prior knowledge of or, indeed, without any prior information about what the true model really is.

However the estimation results suggest that the power of these ``omnibus'' specification test statistics may be low, even with samples as large as N=3000. To see how hard it might be to test this hypothesis, consider figure 1. For example comparing and we find that they are very close in both the probit and logit specifications. Tables 2 and 3 present the estimated values of and for the probit and logit specifications, respectively.

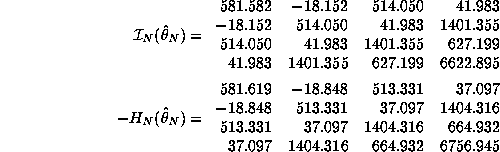
Figure 1 plots the true conditional choice probability , i.e. the probit model evaluated at the true parameters and at the (sorted) x values in the data file data3.asc, the estimated probit and logit models, and the logit model evaluated at the true parameter values . We see that even thought the estimated parameter values for the logit and probit models are significantly different from each other, the estimated choice probabilities are nearly identical for each x in the sample. Indeed the estimated logit and probit choice probabilities are visually virtually indistinguishable. Maximum likelihood is doing its best (in the presence of noise) to try to fit the true choice probability , and we see that both the logit and probit models are sufficiently flexible functional forms that we can approximate the data about equally well with either specification. As a result the maximized value of the log-likelihood is almost identical for both models, i.e. for both the probit and logit specifications. Recalling the discussion of neural networks in our presentation of non-parametric estimation methods, both the logit and probit models can be regarded as simplified neural networks with a single hidden unit and the logistic and normal cdf's as ``squashing functions.'' Given that neural networks can approximate a wide variety of functions, it isn't so surprising that the logit and probit choice probabilities can approximate each other very well, with each yielding virtually the same overall fit. Thus, one can imagine it would be very hard for an omnibus specification test statistic to discern which of these models is the true model generating the data.

Figure 1 also plots the predicted logit choice probabilities that result from evaluating the logit model at the true parameter values . We can see that in this case the choice probabilities of the logit model are quite different from the choice probabilities of the true probit model. However the logit maximum likelihood estimates are not converging to when the model is misspecified. Instead, the misspecified maximum likelihood estimator is converging to the parameter vector which minimizes the Kullback-Liebler distance between the chosen parametric specification and the true choice probability:

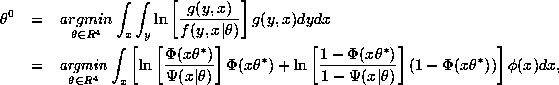
where is the standard normal density, the marginal density of the x variables used to generate the data in this problem. Given the flexibility of the logit specification, we find that is almost identical to the true probit specification even though and are fairly different parameter vectors.

Question 4 We can also use nonlinear least squares to consistently estimate , assuming the specification of the choice probability is correct, since by definition of the conditional choice probability we have:

Thus, is the true conditional expectation function, so even though the dependent variable y only takes on the values we still have a valid regression equation:

where the error term also takes on two possible values , but satisfies by construction. By the general uniform consistency arguments presented in class, it is easy to show that the nonlinear least squares estimator defined by:

will be a consistent estimator of if the model is correctly specified, i.e. if , where is the standard normal CDF, but if the choice probability is misspecified, then with probability 1 we have where is given by:

Question 5 Table 4 presents the NLS estimates of for the logit and probit specifications of using the estimation program estimate.gpr and the procedures log_nls.g and prb_nls.g respectively.

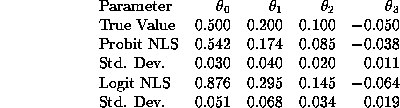
Comparing Tables 1 and 4 we see that the MLE and NLS estimates of are virtually identical for each specification. The standard errors are virtually the same in this case as well. In general the NLS estimator is less efficient than the MLE since the latter attains the Cramer-Rao lower bound when the model is correctly specified. In this case the MLE and NLS estimates happen to be amazingly close to each other, and the standard errors of the NLS estimates are actually minutely smaller than the standard errors of the MLE estimates (for example for the MLE estimator of we have whereas for the NLS estimator we have ). This anomaly is probably not due to a programming error on my part (since running the gradient and hessian check options in estimate.gpr reveals that the analytic formulas I programmed match the numerical values quite closely), but probably due to to a combination of roundoff error and estimation noise. Although the Cramer-Rao lower bound holds asymptotically, it need not hold in finite samples for the sample analog estimates of the covariance matrix, which can be potentially quite noisy estimates of the asymptotic covariance matrix. It is straightforward to show that for the NLS has asymptotic covariance matrix given by:

where

and

whereas for the correctly specified probit model the Cramer-Rao lower bound, , is given by

Thus we have unless the model is homoscedastic, i.e. when for all x, which implies that is a constant for all x, which is almost never the case in any ``interesting'' application. We conclude that the MLE estimator of is necessarily more efficient than the NLS estimator, and the only reason why the NLS has slightly smaller estimated standard errors in this example is due to round-off and estimation error. For other sample sizes, say N=500, we do find that the estimated standard deviations of the MLE estimator are smaller than the NLS estimator. For example when N=500 the NLS estimator of is and its standard error is , whereas the MLE estimator is and its standard error is . Thus, while we do see an efficiency gain to doing maximum likelihood, it is far from overwhelming in this particular case.

Question 6 It is easy to see that the errors in the regression formulation of the binary choice model, are heteroscedastic with conditional variance given by:

(Too see this, note that the conditional variance of and given are the same, and the latter is a Bernoulli random variable that takes on the value with probability . As is well known, a Bernoulli random variable has variance p(1-p)). Thus, we have a case where heteroscedasticity has a known functional form and we can make use of it to compute feasible generalized least squares (FGLS) estimates of . In the first stage we compute the NLS estimates of and using these estimates, call them , we compute estimated conditional variance given by the formula above but with the first stage NLS estimates in place of . Then in the second stage we compute the FGLS estimates as the solution to the following weighted least squares problem:

The FGLS estimates of , computed by log_fgls.g and prb_fgls.g in the logit and probit cases, respectively, are virtually identical to the NLS estimates of , which are in turn virtually identical to the maximum likelihood estimates in the logit and probit specifications presented in Table 1 so I didn't bother to present them here.

Should we conclude from this that there isn't much heteroscedasticity in this problem? Figure 2 plots for this problem and we see that there is indeed substantial heteroscedasticity, with fairly large variation in the effective weighting of the observations. However by plotting the relative contribution of the terms in the weighted and unweighted sum of squared residuals, you will find that except for a small number of observations with the lowest values of which the FGLS estimator assigns very high weights to, the relative sizes of the vast majority of the true squared residuals in both the FGLS and NLS estimators are very similar. This explains why the FGLS and NLS estimators are not very different even though there appears to be substantial heteroscedasticity in this problem.

Question 7 The FGLS estimator is asymptotically equivalent to the maximum likelihood estimator, a result suggested by the fact that the likelihood function and the weighted sum of squared residuals happen to have the same first order conditions:

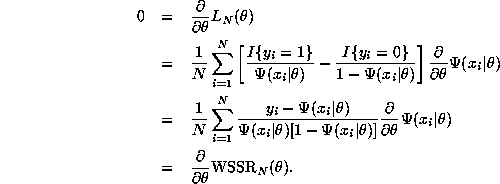
Actually, the first order conditions are only identical for the continuously updated version of the FGLS estimator, where instead of using a first stage NLS estimate to make an estimated correction for heteroscedasticity, we continually update our estimate of the heteroscedasticity as changes, so the same appears in the numerator and denominator terms in the third equation above whereas in the FGLS estimator appears in the denominator terms. However recalling the logic of the ``Amemiya correction'' we need to consider whether it is necessary to account for the estimation noise in the first stage estimates in deriving the asymptotic distribution of the FGLS estimator, . It will turn out that there is a form of ``block diagonality'' here which enables the FGLS estimator to be ``adaptive'' in the sense that the asymptotic distribution of the FGLS estimator does not depend on whether we use the noisy first stage NLS estimator to compute a noisy estimate of the conditional variance to use as weights, or if we use the true conditional variance .

Before we show this, we first show that if we did use the true conditional variance as the weights in the FGLS estimator, it would be as efficient as maximum likelihood: i.e. the FGLS estimator attains the Cramer-Rao lower bound. To see this do a Taylor-series expansion of the first order condition for the FGLS estimator about :

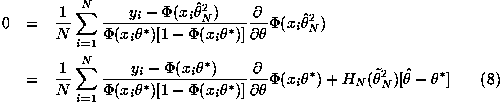
where is on the line segment between and and

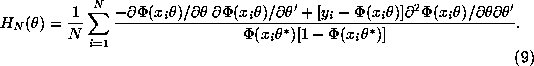
By the uniform Strong Law of Large Numbers, we have that with probability 1 where

Since with probability 1, it follows that with probability 1. Using the law of iterated expectations we can show that the second term in the above expectation is zero when so that

The Central Limit Theorem implies that

where it is easy to see that . Combining all results in equations we see that the asymptotic distribution of the FGLS estimator is given by:

Thus the asymptotic covariance matrix of the FGLS estimator is the inverse of the information matrix (see equation 6), so it is asymptotically efficient.

Now we need to show that if we computed the FGLS estimator using the (inverse of) the estimated conditional variance instead of the true conditional variance as weights, the asymptotic distribution is still the same as that given in (13) above. We do this using the same logic as for the general derivation of the ```Amemiya correction'', Taylor expanding the FGLS FOC in both variables and about their limiting value . That is, if we define the function by

then we have the following joint Taylor series expansion for about

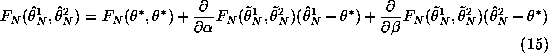
We know that the NLS estimator is asymptotically normal, so , i.e. it is bounded in probability. Thus, the FGLS estimator that uses estimated conditional variance as weights will have the same asymptotic distribution as the (infeasible) FGLS estimator that of the true conditional variance as weights if we can show that with probability 1 we have:

But this follows from the USLLN and the consistency of and .

Question 8 Figure 3 presents a comparison of the true choice probability and nonparametric estimates of this probability using both kernel and series estimators from the program kernel.gpr.

The series estimator seems to provide a better estimator of the true choice probability than the kernel density estimator in this case. The series estimator is just the predicted value from a simple OLS regression of the on a constant and the first 3 powers of :

and the kernel estimator is the standard Nadaraya-Watson estimator

where and is defined to be a Gaussian density function. For the choice of a bandwidth parameter, a rule of thumb is used: with In this case the automatically chosen bandwith turned out to be . The series estimator is much faster to compute than the kernel estimator, since the above summations must be carried out for each of the N=3000 observations in the sample in order to plot the estimated choice probability for each observation. Comparing the fit of the parametric and nonparametric models in figures 1 and 2, we see that even though the logit and probit models are ``parametric'', they have sufficient flexibility to enable them to provide a better fit than either the kernel density or series estimators. This conclusion is obviously specific to this example where the true conditional choice probability was generated by a probit model, and as we saw from figure 1, one can adjust the parameters to make the predicted probabilities of the logit and probit models quite close to each other.

Figure 4 plots the estimated choice probabilities produced by both the probit and logit maximum likelihood estimates and the kernel and series nonparametric estimates. We see that except for the ``hump'' in the kernel density estimate, all the estimates are very close to each other. It would appear to be quite difficult to say which estimate was the ``correct'' one: instead we conclude that 4 different ways of estimating the conditional choice probability give approximately the same results.

• About this document ...