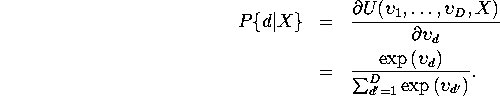Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27

PROBLEM SET 3: SOLUTIONS

Classical Methods (I)

QUESTION 1 Since is symmetric, positive definite, there exists Cholesky decomposition P such that

Now we know vector , and each element of Z , for all . Therefore,

QUESTION 2 Since

log likelihood function for can be written as

MLE of , , satisfies

Therefore

QUESTION 3

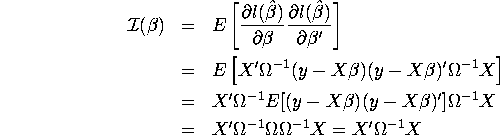
Therefore

QUESTION 4 Define

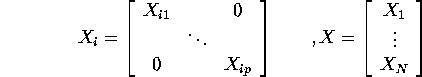
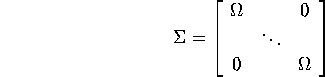
We know that GLS estimator and its covariance matrix can be written as follows;

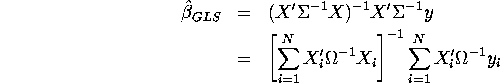
Note this is stacked observation by observation. Now OLS estimators equation by equation can be written with matrices stacked by equation by equation as follows;

where

But since

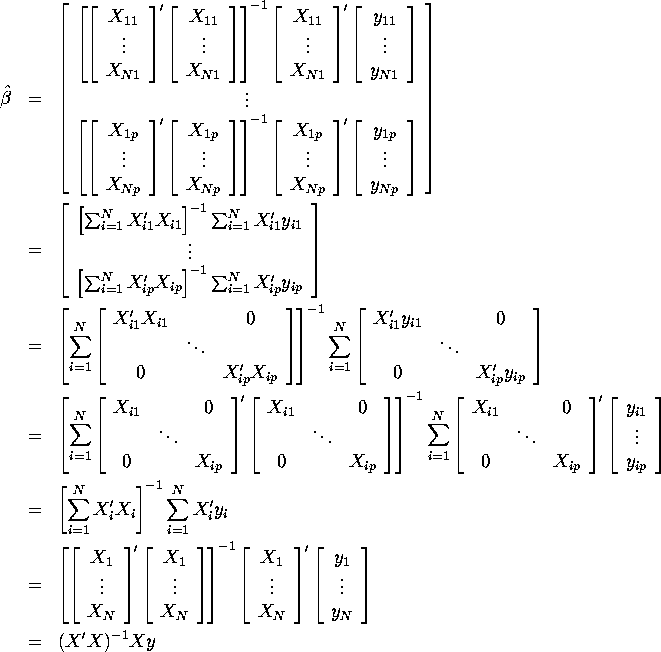
Therefore

QUESTION 5

A.

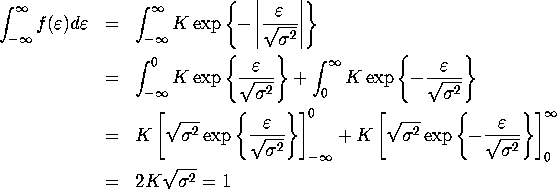
Therefore

B. Since

log likelihood function for can be written as

Therefore

QUESTION 6 The conditional posterior for , , is proportional to , and the latter is given by:

By completing the square,

i.e. the conditional density of given is .

2. The conditional posterior for , , is prortional to , which is given by:

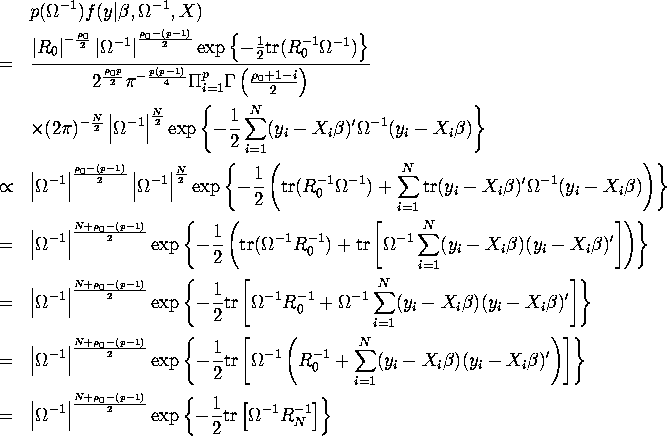
Therefore

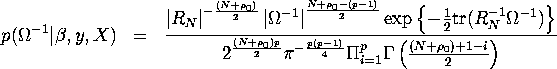
i.e. the density of given is .

QUESTION 7

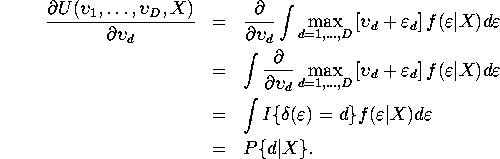
QUESTION 8 From Mood-Graybill-Boes(1974,p542), the mean of extreme value distribution with CDF

is . We know

First, we derive CDF of .

Since this is CDF of extreme value distribution, the extreme value family is max-stable, and the mean of can be written as

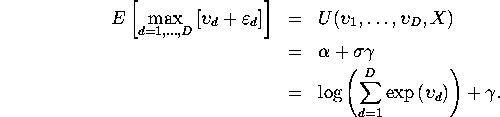
By Williams-Daly-Zachary Theorem,

• About this document ...