


Next: About this document
Spring 1998 John Rust
Economics 551b 37 Hillhouse, Rm. 27
PROBLEM SET 1
Nonlinear Estimation of Binary Choice Models
QUESTION 1 Extract data in data3.asc in
the
pub/John_Rust/courses/econ551/regression/
directory on gemini.econ.yale.edu (either ftp to
gemini.econ.yale.edu and login as ``anonymous'' and
cd pub/John_Rust/courses/econ551/regression and
get data1.asc or click on the hyperlink in the html
version of this document). This data file
contains n=3000 IID
observations 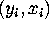 that I generated from the
binary probability model:
that I generated from the
binary probability model:
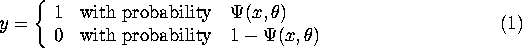
where 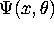 is some parametric model of the conditional probability
of the binary variable y given x, i.e.
is some parametric model of the conditional probability
of the binary variable y given x, i.e. 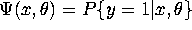 .
Two standard models for
.
Two standard models for 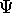 are the logit and probit
models. In the logit model we have
are the logit and probit
models. In the logit model we have

and in the probit mode we have

where 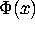 is the standard normal CDF, i.e.
is the standard normal CDF, i.e.
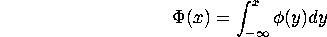
where
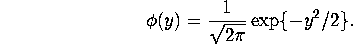
More generally, 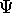 could take the form
could take the form

where F is an arbitrary continuous CDF.
- 1.
- Show that versions
of the logit and probit models can be derived from an underlying
random utility model where a decision maker has utility
function of the form:
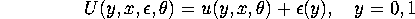
and takes action y=1 if  and takes action y=0 if
and takes action y=0 if 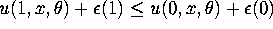 .
Derive the implied choice probability
.
Derive the implied choice probability 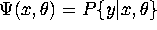 in the case
where
in the case
where 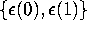 is a bivariate normal random
vector with
is a bivariate normal random
vector with 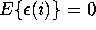 ,
, 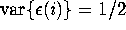 and
and 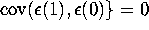 and
and 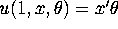 and
and 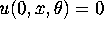 .
What is the form of
.
What is the form of 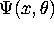 in the general case when
in the general case when
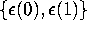 has an unrestricted bivariate normal distribution
with mean vector
has an unrestricted bivariate normal distribution
with mean vector 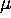 and covariance matrix
and covariance matrix 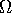 ? If the utility
function includes a constant term, i.e.
? If the utility
function includes a constant term, i.e. 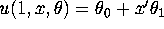 are the
are the 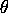 ,
, 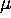 and
and 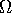 parameters all separately identified
if we only have access to data on (y,x) pairs?
parameters all separately identified
if we only have access to data on (y,x) pairs?
- 2.
- Derive the form of the choice probability
under the same assumptions are part 1 above
but when
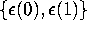 has a bivariate Type I extreme value distribution by doing problem
7 of the 1997 Econ 551 problem set 3. By doing this you will have derived
the binary logit model from first principles.
has a bivariate Type I extreme value distribution by doing problem
7 of the 1997 Econ 551 problem set 3. By doing this you will have derived
the binary logit model from first principles.
- 3.
- Using the artificially generated data in
pub/John_Rust/courses/econ551/regression/data3.asc
compute maximum likelihood estimates of
the parameters 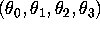 of
the logit and probit specifications given in equations (2) and (3) above,
where
of
the logit and probit specifications given in equations (2) and (3) above,
where 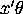 is given by:
is given by:
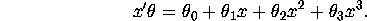
- 4.
- Is it possible to consistently estimate
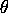 by doing
nonlinear least squares estimation of the nonlinear regression formulation
of the binary probability model
by doing
nonlinear least squares estimation of the nonlinear regression formulation
of the binary probability model

instead of doing maximum likelihood? If so, provide a proof of the
consistency of the NLLS estimator. If not, provide a counterexample
showing that the NLLS estimator is inconsistent.
- 5.
- Estimate both the probit and logit specifications by nonlinear
least squares as suggested in part (4). How do the parameter estimates
and standard errors compare to the maximum likelihood estimates computed
in part 3?
- 6.
- Is there any problem of heteroscedasticity in the nonlinear
regression formulation of the problem in (4)? If so, derive the form
of the heteroscedasticity and, using the estimated ``first stage''
parameters from part 5 above, compute second stage ``feasible
generalized least squares'' (FGLS) estimates of
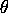 .
.
- 7.
- Are the FGLS estimates of
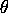 consistent and asymptotically
normally distributed (assuming the model is correctly specified)?
If so, derive the asymptotic distribution of the
FGLS estimator, and if not provide a counter example showing that
the FGLS estimator is inconsistent or not asymptotically normally
distributed. If you conclude that the FGLS estimator is asymptotically
normally distributed, is it as efficient as the maximum likelihood estimator
of
consistent and asymptotically
normally distributed (assuming the model is correctly specified)?
If so, derive the asymptotic distribution of the
FGLS estimator, and if not provide a counter example showing that
the FGLS estimator is inconsistent or not asymptotically normally
distributed. If you conclude that the FGLS estimator is asymptotically
normally distributed, is it as efficient as the maximum likelihood estimator
of 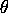 ? Explain your reasoning for full credit.
? Explain your reasoning for full credit.
- 8.
- Is it possible to determine whether the data in the file
data3.asc are generated from a logit or probit model? In answering
this question, consider whether you could estimate
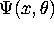 nonparametrically via non-parametric regression. Is there any way you
could use the nonparametric regression estimate of
nonparametrically via non-parametric regression. Is there any way you
could use the nonparametric regression estimate of 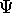 to help
discriminate between the logit and probit specifications?
to help
discriminate between the logit and probit specifications?



Next: About this document
John Rust
Sat Mar 21 13:09:15 CST 1998
![]() that I generated from the
binary probability model:
that I generated from the
binary probability model:
![]()
![]() is some parametric model of the conditional probability
of the binary variable y given x, i.e.
is some parametric model of the conditional probability
of the binary variable y given x, i.e. ![]() .
Two standard models for
.
Two standard models for ![]() are the logit and probit
models. In the logit model we have
are the logit and probit
models. In the logit model we have
![]()
![]()
![]() is the standard normal CDF, i.e.
is the standard normal CDF, i.e.
![]()
![]()
![]() could take the form
could take the form
![]()
![]()
![]() and takes action y=0 if
and takes action y=0 if ![]() .
Derive the implied choice probability
.
Derive the implied choice probability ![]() in the case
where
in the case
where ![]() is a bivariate normal random
vector with
is a bivariate normal random
vector with ![]() ,
, ![]() and
and ![]() and
and ![]() and
and ![]() .
What is the form of
.
What is the form of ![]() in the general case when
in the general case when
![]() has an unrestricted bivariate normal distribution
with mean vector
has an unrestricted bivariate normal distribution
with mean vector ![]() and covariance matrix
and covariance matrix ![]() ? If the utility
function includes a constant term, i.e.
? If the utility
function includes a constant term, i.e. ![]() are the
are the ![]() ,
, ![]() and
and ![]() parameters all separately identified
if we only have access to data on (y,x) pairs?
parameters all separately identified
if we only have access to data on (y,x) pairs?
![]() of
the logit and probit specifications given in equations (2) and (3) above,
where
of
the logit and probit specifications given in equations (2) and (3) above,
where ![]() is given by:
is given by:
![]()
![]()