Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27
PROBLEM SET 3
Classical Methods(I)
(Due: February 24, 1997)
QUESTION 1
Let ![]() where Y is
where Y is ![]() random vector
and
random vector
and ![]() is
is ![]() positive definite matrix. Prove
positive definite matrix. Prove ![]() .
.
QUESTION 2 Suppose regression model
![]()
(where y, ![]() are
are ![]() , X is
, X is ![]() , and
, and ![]() is
is ![]() ) with normality assumption on disturbance,
) with normality assumption on disturbance, ![]() . Derive the maximum likelihood estimator
(MLE) of
. Derive the maximum likelihood estimator
(MLE) of ![]() when
when ![]() is known, and show that MLE is
identical to the GLS estimator.
is known, and show that MLE is
identical to the GLS estimator.
QUESTION 3
Show that the Cramer-Rao lower bound, ![]() , corresponds to the GLS
covariance matrix,
, corresponds to the GLS
covariance matrix, ![]() , in
Question 2.
, in
Question 2.
QUESTION 4 Suppose following SUR model,

where ![]() is
is ![]() ,
, ![]() ,
, ![]() is
is ![]() , and
, and ![]() . Also suppose covariance matrix
of
. Also suppose covariance matrix
of ![]() is
is ![]() . Derive the covariance matix of
. Derive the covariance matix of ![]() OLS estimator
OLS estimator ![]() ,
and show this covariance matrix is larger than that of GLS estimator,
,
and show this covariance matrix is larger than that of GLS estimator, ![]() .
.
QUESTION 5 Derive the maximum likelihood estimator for the model
![]()
where ![]() are IID double exponential random
variables with mean 0 and scale parameter
are IID double exponential random
variables with mean 0 and scale parameter ![]() :
:
![]()
Hint: Show
that the MLE for ![]() is identical to the Least Absolute Deviations
estimator
is identical to the Least Absolute Deviations
estimator ![]() defined by:
defined by:
![]()
QUESTION 6
(Bayesian) Suppose ![]() in SUR
model of Question 4. Suppose the prior for the parameters
in SUR
model of Question 4. Suppose the prior for the parameters
![]() is given by the product of two
independent priors for the
is given by the product of two
independent priors for the ![]() vector
vector ![]() and the
and the
![]() inverse covariance matrix
inverse covariance matrix ![]() :
:
![]()
Suppose ![]() i.e. the prior
for
i.e. the prior
for ![]() is a multivariate normal distribution with hyperparameters
is a multivariate normal distribution with hyperparameters
![]() (the mean of the prior) and
(the mean of the prior) and ![]() (the covariance matrix
of the prior). Suppose
(the covariance matrix
of the prior). Suppose ![]() , i.e. the
prior for
, i.e. the
prior for ![]() is a Wishart distribution with hyperparameters
is a Wishart distribution with hyperparameters
![]() (
( ![]() ) and
) and ![]() (
( ![]() ). Recall that the
density of a Wishart is given by:
). Recall that the
density of a Wishart is given by:
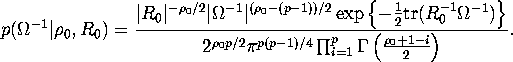
Show that the posterior distribution of ![]() is conditionally conjugate
i.e. it can be decomposed as a product of a Normal and Wishart as follows:
is conditionally conjugate
i.e. it can be decomposed as a product of a Normal and Wishart as follows:
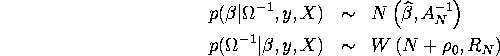
where
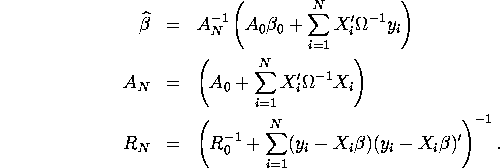
Hint: Show that the likelihood function can be expressed as:
![]()
where ![]() is
is ![]() and
and ![]() is
is ![]() . Also use the fact
that
. Also use the fact
that ![]() so we can write:
so we can write:
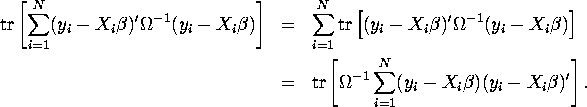
QUESTION 7
Consider the random utility model:
where
where
i.e.
where
Definition: The Social Surplus Function
The Social Surplus function is the expected maximized utility of the
agent.
Problem: Prove the Williams-Daly-Zachary Theorem:
and discuss its relationship to Roy's Identity.
Hint: Interchange the differentiation and expectation
operations when computing
and show that
Question 8 Consider the special case of
the random utility model when
Show that the conditional choice probability
Hint 1: Use the Williams-Daly-Zachary Theorem, showing
that in the case of the extreme value distribution (8) the Social
Surplus function is given by
where
Hint 3: Let ![]()
![]() is a decision-maker's payoff or utility for selecting
alternative d from a set containing D possible alternatives (we
assume that the individual only chooses one item). The term
is a decision-maker's payoff or utility for selecting
alternative d from a set containing D possible alternatives (we
assume that the individual only chooses one item). The term ![]() is
known as the deterministic or strict utility from alternative
d and the error term
is
known as the deterministic or strict utility from alternative
d and the error term ![]() is the random component of
utility. In empirical applications
is the random component of
utility. In empirical applications ![]() is often specified as
is often specified as
![]()
![]() is a vector of observed covariates and
is a vector of observed covariates and ![]() is a vector
of coefficients determining the agent's utility to be estimated. The
interpretation is that
is a vector
of coefficients determining the agent's utility to be estimated. The
interpretation is that ![]() represents a vector of characteristics
of the decision-maker and alternative d that are observable
by the econometrician and
represents a vector of characteristics
of the decision-maker and alternative d that are observable
by the econometrician and ![]() represents characteristics
of the agent and alternative d that affect the utility of choosing
alternative d which are unobserved by the econometrician. Define
the agent's decision rule
represents characteristics
of the agent and alternative d that affect the utility of choosing
alternative d which are unobserved by the econometrician. Define
the agent's decision rule ![]() by:
by:
![]()
![]() is the optimal choice for an agent whose
unobserved utility components are
is the optimal choice for an agent whose
unobserved utility components are
![]() . Then the agent's choice
probability
. Then the agent's choice
probability ![]() is given by:
is given by:
![]()
![]() is the vector of observed characteristics of
the agent and the D alternatives and
is the vector of observed characteristics of
the agent and the D alternatives and ![]() is the
conditional density function of the random components of utility given
the values of observed components X, and
is the
conditional density function of the random components of utility given
the values of observed components X, and ![]() is the indicator function given by
is the indicator function given by ![]() if
if ![]() and 0 otherwise.
Note that the integral above is
actually a multivariate integral over the D components of
and 0 otherwise.
Note that the integral above is
actually a multivariate integral over the D components of
![]() , and simply represents the
probability that the values of the vector of unobserved utilities
, and simply represents the
probability that the values of the vector of unobserved utilities ![]() lead the agent to choose alternative d.
lead the agent to choose alternative d.
![]() is given by:
is given by:
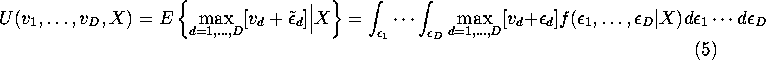

![]()
![]() :
:
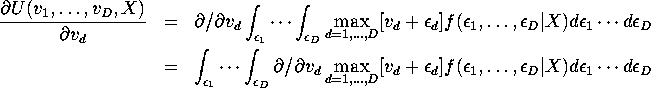
![]()
![]() has a multivariate (Type I) extreme value distribution:
has a multivariate (Type I) extreme value distribution:
![]()
![]() is given by
the multinomial logit formula:
is given by
the multinomial logit formula:
![]()
![]()
![]() is Euler's constant.
is Euler's constant.
Hint 2: To derive equation (9) show that the
extreme value family is max-stable: i.e. if ![]() are IID extreme value random variables, then
are IID extreme value random variables, then
![]() also has an extreme value distribution. Also
use the fact that the expectation of a single extreme value random
variable with location parameter
also has an extreme value distribution. Also
use the fact that the expectation of a single extreme value random
variable with location parameter ![]() and scale parameter
and scale parameter
![]() is given by:
is given by:
![]()
and the CDF is given by
![]()
![]() be
INID (independent, non-identically distributed) extreme value
random variables with location parameters
be
INID (independent, non-identically distributed) extreme value
random variables with location parameters ![]() and common scale parameter
and common scale parameter ![]() . Show that this family is
max-stable by proving that
. Show that this family is
max-stable by proving that ![]() is an extreme
value random variable with scale parameter
is an extreme
value random variable with scale parameter ![]() and location parameter
and location parameter
![]()
![]()
![]()
![]()
Next: About this document