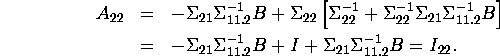Woocheol Kim
Jan. 31, 1998
Question 1
A. Step 1
Under the assumption that 
and 
are
finite, 
is well-defined. Now, let 
Then,
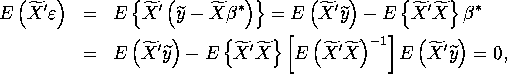
as is required.
B. Step 2
After plugging in 
and
using the definition of covariance, we get
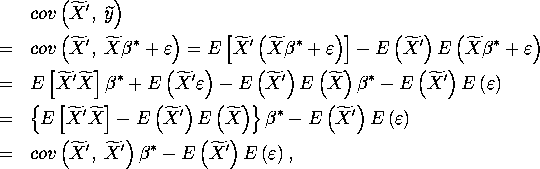
where the 3rd equality comes from the result of Step 1. Thus,
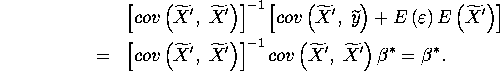
C. Step 3
When 
or 
the above result implies
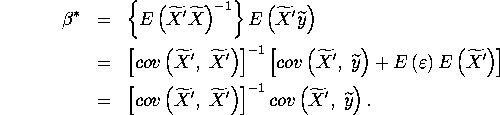
D. Step 4
The general form of the joint normal density is
Let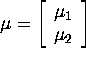 
and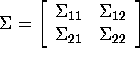 
be a partition according to 
Note that
Also, we can easily verify that
from postmultiplying 
by the inverse matrix.(The verfication can be
found at the end of this solution.)
Insert 1 and 2into the joint normal density, and it will give
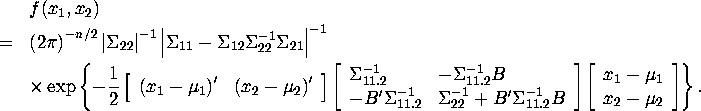
First, by definitionthe second determinant 
Next, calculate the product of three matrices inside the exp. function. It
is equal to
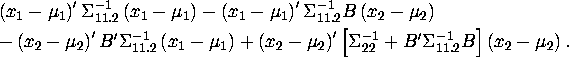
If we extract the forth term, 
that consists of the second
subgroup of random variables, 
the remaining term can be rewritten
as
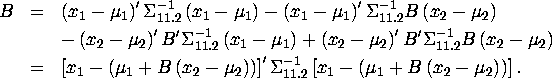
Therefore, the joint density can be decomposed into 
where
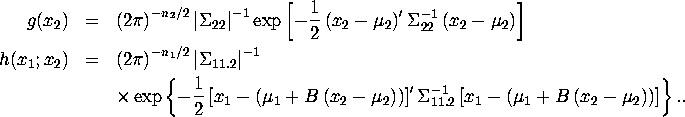
It is obvious that 
is the normal density of 
with mean 
and variance 
and 
is the normal
density of 
with mean 
and
variance 
when is a constant. Let 
be the marginal density of 
Then,
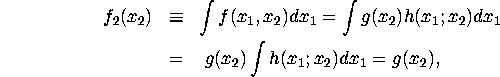
since is a density. Now, it follows that
Also, the conditional density 
that is,
If we apply the above result on conditional distribution to the case where 
has a joint multivariate normal
distribution, then, the conditional distribution of 
given 
is
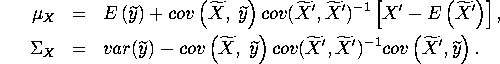
Hence, when by Step 3,
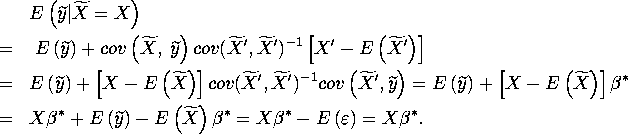
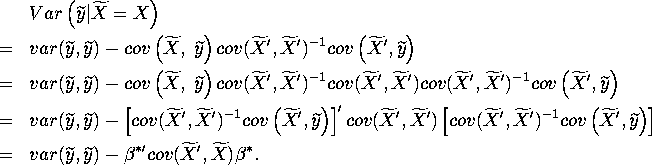
Appendix.
The inverse of a partitioned matrix:
Consider the multiplication,\
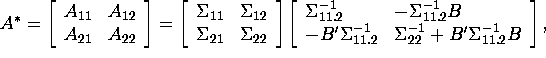
with 
It suffices to confirm that 
i.e., 
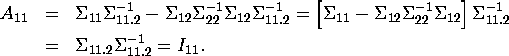
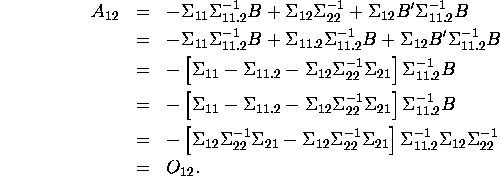
