


Next: About this document ...
Spring 2001 John Rust
Economics 551b 37 Hillhouse, Rm. 27
SOLUTIONS TO FINAL EXAM
April 27, 2001
Part I: 15 minutes, 15 points. Answer all questions below:
1. Suppose
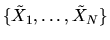 are IID draws from a
are IID draws from a
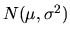 distribution (i.e. a normal
distribution with mean
distribution (i.e. a normal
distribution with mean 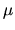 and variance
and variance 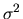 ). Consider the
estimator
). Consider the
estimator
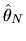 defined by:
defined by:
 |
(1) |
Which of the
following statements are true and which are false?
To answer this, note that the sample mean of the
N IID/ observations
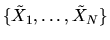 ,
,
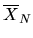 is distributed as
is distributed as
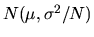 .
Then
.
Then
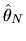 is the square of
is the square of
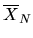 and is thus a
non-central
and is thus a
non-central 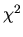 random variable. Its expectation is
random variable. Its expectation is
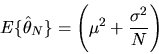 |
(2) |
and its variance is
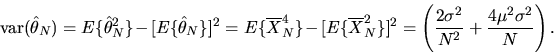 |
(3) |
Thus it is clear that
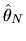 converges in probability to
converges in probability to
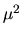 and is an upward biased estimator of
and is an upward biased estimator of 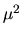 .
These conclusions
would follow even if the Xi's were not normally distributed. In
that case we would use the continuous mapping theorem and the fact
that
.
These conclusions
would follow even if the Xi's were not normally distributed. In
that case we would use the continuous mapping theorem and the fact
that
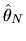 is a continuous function (x2) of the sample
mean
is a continuous function (x2) of the sample
mean
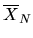 ,
and thus,
,
and thus,
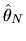 converges in probability
to
converges in probability
to 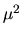 is a simple application of the continuous mapping theorem.
Also since the function x2 is convex, Jensen's inequality can be
used to show that
is a simple application of the continuous mapping theorem.
Also since the function x2 is convex, Jensen's inequality can be
used to show that
![\begin{displaymath}E\{\hat\theta_N\}= E\{ [\overline X_N]^2\} > [E\{\overline X_N\}]^2 =
\mu^2.
\end{displaymath}](img13.gif) |
(4) |
From these results the following true and false answers should now
be obvious:
- A.
-
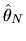 is a consistent estimator of
is a consistent estimator of 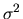 .
False.
.
False.
- B.
-
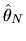 is an unbiased estimator of
is an unbiased estimator of 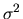 .
False.
.
False.
- C.
-
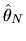 is a consistent estimator of
is a consistent estimator of 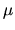 .
False.
.
False.
- D.
-
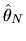 is an unbiased estimator of
is an unbiased estimator of 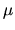 .
False.
.
False.
- E.
-
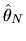 is a consistent estimator of
is a consistent estimator of 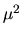 .
True.
.
True.
- F.
-
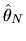 is an unbiased estimator of
is an unbiased estimator of 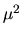 .
False.
.
False.
- G.
-
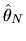 is an upward biased estimator of
is an upward biased estimator of 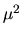 .
True.
.
True.
- H.
-
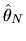 is a downward biased estimator of
is a downward biased estimator of 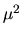 .
False.
.
False.
2. Consider estimation of the linear model
 |
(5) |
based on N IID observations
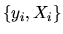 where Xi is a
where Xi is a
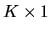 vector of independent variables and yi is a
vector of independent variables and yi is a
 scalar independent variable.
Mark each of the following statements as true or false:
scalar independent variable.
Mark each of the following statements as true or false:
- A.
- The Gauss-Markov Theorem proves that the ordinary
least squares estimator (OLS) it BLUE (Best Linear Unbiased
Estimator). True.
- B.
- The Gauss-Markov Theorem requires that the error term
in the regression
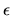 be normally distributed with mean 0 and
variance
be normally distributed with mean 0 and
variance 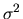 .
False.
.
False.
- C.
- The Gauss-Markov Theorem does not apply if the true
regression function does not equal
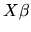 ,
i.e. if
,
i.e. if
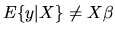 .
True.
.
True.
- D.
- The Gauss-Markov Theorem does not apply if there is
heteroscedasticity. True.
- E.
- The Gauss-Markov Theorem does not apply if the error term
has a non-normal distribution. False.
- F.
- The maximum likelihood estimator of
 is more efficient
than the OLS estimator of
is more efficient
than the OLS estimator of  .
True.
.
True.
- G.
- The OLS estimator of
 will be unbiased only if the
error terms are distributed independently of X and have mean 0.
False.
will be unbiased only if the
error terms are distributed independently of X and have mean 0.
False.
- H.
- The maximum likelihood estimator of
 is the same as
OLS only in the case where
is the same as
OLS only in the case where 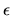 is normally distributed. True.
is normally distributed. True.
- I.
- The OLS estimator will be a consistent estimator of
 even if the error term
even if the error term 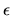 is not normal and even if there
is heteroscedasticity. True.
is not normal and even if there
is heteroscedasticity. True.
- J.
- The OLS estimator of the asymptotic covariance matrix for
 ,
,
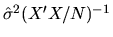 (where
(where
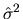 is the sample variance
of
the estimated residuals
is the sample variance
of
the estimated residuals
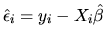 )
is a consistent estimator regardless of whether
)
is a consistent estimator regardless of whether 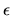 is normally
distributed or not. True.
is normally
distributed or not. True.
- K.
- The OLS estimator of the asymptotic covariance matrix for
 ,
,
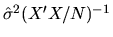 (where
(where
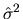 is the sample variance
of
the estimated residuals
is the sample variance
of
the estimated residuals
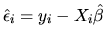 )
is a consistent estimator regardless of whether there is
heteroscedasticity in
)
is a consistent estimator regardless of whether there is
heteroscedasticity in 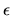 .
False.
.
False.
- L.
- If the distribution of
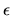 is double exponential,
i.e. if
is double exponential,
i.e. if
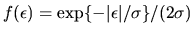 ,
the maximum
likelihood estimator of
,
the maximum
likelihood estimator of  is the Least Absolute Deviations
estimator and it is asymptotically efficient relative to the OLS
estimator. True.
is the Least Absolute Deviations
estimator and it is asymptotically efficient relative to the OLS
estimator. True.
- M.
- The OLS estimator cannot be used if the regression function
is misspecified, i.e. if the true regression function
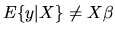 .
False.
.
False.
- N.
- The OLS estimator will be inconsistent if
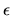 and X are correlated. True.
and X are correlated. True.
- O.
- The OLS estimator will be inconsistent if the
dependent variable y is truncated, i.e. if the dependent variable
is actually determined by the relation
![\begin{displaymath}y= \max[0, X\beta + \epsilon] \end{displaymath}](img27.gif) |
(6) |
True.
- P.
- The OLS estimator is inconsistent if
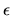 has
a Cauchy distribution, i.e. if the density of
has
a Cauchy distribution, i.e. if the density of 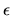 is given
by
is given
by
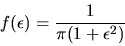 |
(7) |
True.
- Q.
- The 2-stage least squares estimator is a better estimator
than the OLS estimator because it has two stages and is therefore
twice as efficient. False.
- R.
- If the set of instrumental variables W and the set of
regressors X in the linear model coincide, then 2 stage least squares
estimator of
 is the same as the OLS estimator of
is the same as the OLS estimator of  .
True.
.
True.
Part II: 30 minutes, 30 points. Answer 2 of the
following 6 questions below.
QUESTION 1 (Probability question) Suppose  is a
is a
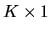 random
vector with a multivariate N(0,I) distribution, i.e.
random
vector with a multivariate N(0,I) distribution, i.e.
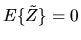 where
0 is a
where
0 is a
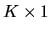 vector of zeros and
vector of zeros and
 where I is the
where I is the
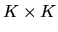 identity matrix. Let M be a
identity matrix. Let M be a
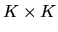 idempotent matrix, i.e. a matrix that satisfies
idempotent matrix, i.e. a matrix that satisfies
Show that
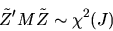 |
(9) |
where 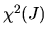 denotes a chi-squared random variable with
J degrees of freedom and
denotes a chi-squared random variable with
J degrees of freedom and
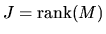 .
Hint: Use the fact that
M has a singular value decomposition,
i.e.
.
Hint: Use the fact that
M has a singular value decomposition,
i.e.
where X' X = I and D is a diagonal matrix whose diagonal elements
are equal to either 1 or 0.
Answer: Let X be the
 orthonormal matrix
in the singular value decompostion of the idempotent matrix M. Since
X'X=I, it follows that
orthonormal matrix
in the singular value decompostion of the idempotent matrix M. Since
X'X=I, it follows that
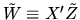 is N(0,I). Thus,
is N(0,I). Thus,
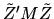 can be rewritten as
can be rewritten as
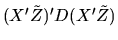 .
Since D is
a diagonal matrix with J 1's K - J 0's on its main diagonal,
it follows that
.
Since D is
a diagonal matrix with J 1's K - J 0's on its main diagonal,
it follows that
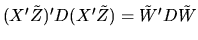 algebraically the sum of J IDD N(0,1) random variables and
thus has a
algebraically the sum of J IDD N(0,1) random variables and
thus has a 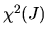 distribution. That is, assuming without loss of
generality that the first J elements of the diagonal of D are 1's
and the remaining K-J elements are 0's we have
distribution. That is, assuming without loss of
generality that the first J elements of the diagonal of D are 1's
and the remaining K-J elements are 0's we have
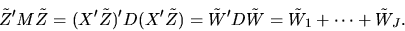 |
(11) |
Since the
 are IID N(0,1)'s, the result
follows.
are IID N(0,1)'s, the result
follows.
QUESTION 2 (Markov Processes)
- A.
- (10%) Are Markov processes of any use in econometrics? Describe
some examples of how Markov processes are used in econometrics such
as providing models of serially dependent data, as a framework for establishing
convergence of estimators and
proving laws of large numbers, central limit theorems, etc.
and as computational tool for doing simulations.
- B.
- (10%) What is a random walk? Is a random walk always a Markov process?
If not, provide a counter-example.
- C.
- (40%) What is the ergodic or invariant distribution of
a Markov process? Do all Markov processes have invariant
distributions? If not, provide a counterexample of a Markov
process that doesn't have an invariant distribution. Can
a Markov process have more than 1 invariant distribution?
If so, give an example.
- D.
- (40%) Consider the discrete Markov process
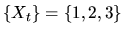 with transition
probability
with transition
probability
Does this process have an invariant distribution? If so,
find all of them.
ANSWERS:
- A.
- Markov processes play a major role in econometrics, since
they it provides one of the simplest yet most
general frameworks for modeling temporal dependence. Markov processes
are used extensively in time series econometrics, since there are
laws of large numbers and central limit theorems that apply to very
general classes of Markov processes that satisfy a ``geometric
ergodicity'' condition. Markov processes are also used extensively
in Gibbs Sampling, which is a technique for simulating draws from
a posterior distribution in econometric models where the posterior
has no convenient analytical solution.
- B.
- A random walk
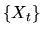 is a special type of Markov process that is
represented as
is a special type of Markov process that is
represented as
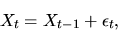 |
(12) |
where
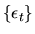 is an IID process that is independent
of
is an IID process that is independent
of 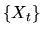 .
If
.
If
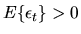 the random walk has positive drift and if
the random walk has positive drift and if
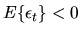 it has negative drift. A random walk is always a Markov process,
since Xt-1 is a sufficient statistic for determining the
probability
distribution of Xt, and previous values
it has negative drift. A random walk is always a Markov process,
since Xt-1 is a sufficient statistic for determining the
probability
distribution of Xt, and previous values
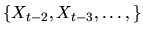 are irrelevant. If F is the CDF for
are irrelevant. If F is the CDF for
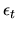 ,
then the Markov transition
probability for
,
then the Markov transition
probability for 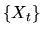 is given by
is given by
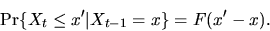 |
(13) |
- C.
- If a Markov Process has a transition probabilty P(x'|x),
then its invariant distribution
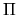 is defined by
is defined by
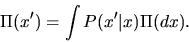 |
(14) |
What this equation says is that if
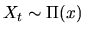 (i.e. Xt is
distributed according to the probability distribution
(i.e. Xt is
distributed according to the probability distribution  ), then
Xt+1 is also distributed according to this same probability
distribution. Not all Markov processes have invariant distributions.
A random walk does not have an invariant distribution, i.e. there
is no solution to the equation (14) above. To see
this, note in particular that due to the independence between
Xt-1 and
), then
Xt+1 is also distributed according to this same probability
distribution. Not all Markov processes have invariant distributions.
A random walk does not have an invariant distribution, i.e. there
is no solution to the equation (14) above. To see
this, note in particular that due to the independence between
Xt-1 and
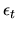 we have
we have
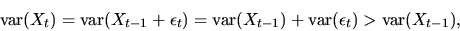 |
(15) |
so that regardless of what distribution Xt-1 has,
it is impossible for Xt to have this same distribution.
- D.
- The transition probability matrix P for this process is given
by the following
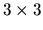 matrix
matrix
![\begin{displaymath}P= \left[ \begin{array}{ccc}
1/2 & 1/3& 1/6 \\
3/4 & 0 & 1/4 \\
0 & 1 & 0 \end{array} \right] \end{displaymath}](img57.gif) |
(16) |
The invariant probability is the solution  to the
to the
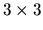 system of equations
system of equations
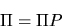 |
(17) |
We can write this out as
You can verify the the unique non-zero solution to the above system of
equations is
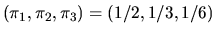 ,
i.e. the unique
invariant distribution is the same as the first row of P.
,
i.e. the unique
invariant distribution is the same as the first row of P.
QUESTION 3 (Consistency of M-estimator)
Consider an M-estimator defined by:
Suppose following two conditions are given
(i) (Identification) For all
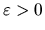
where
 .
.
(ii) (Uniform Convergence)
Prove consistency of the estimator by showing
ANSWER Uniform convergence in probability can
be stated formally as follows: for any
 we have
we have
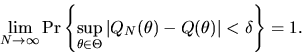 |
(19) |
Now, given any
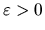 ,
define
,
define 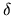 by
by
 |
(20) |
The identification assumption implies that
 .
Now, we want
to show that for any
.
Now, we want
to show that for any
 we have
we have
 |
(21) |
Notice if
 then we have
then we have
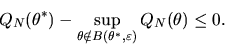 |
(22) |
So it is sufficient to show that uniform convergence implies that
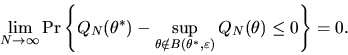 |
(23) |
Using the  defined in equation
(20) and the definition of
uniform convergence in probability in equation (19), we have
defined in equation
(20) and the definition of
uniform convergence in probability in equation (19), we have
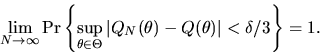 |
(24) |
Thus, for N sufficiently large, the following inequalities
will hold with probability arbitrarily close to 1,
Combining the above inequalities,
it follows that the following inequality
will hold with probability arbitrarily close to 1 for Nsufficiently large:
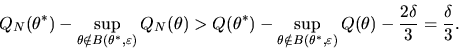 |
(26) |
This implies that
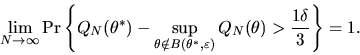 |
(27) |
Since 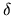 is arbitrary, this implies that
is arbitrary, this implies that
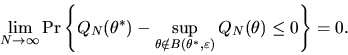 |
(28) |
Since the event that
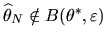 is a subset of the event that
is a subset of the event that
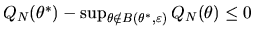 ,
it follows that the limit in
equation (19) holds, i.e.
,
it follows that the limit in
equation (19) holds, i.e.
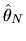 is a
consistent estimator of
is a
consistent estimator of  .
.
QUESTION 4 (Time series question)
Suppose 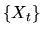 is an ARMA(p,q) process, i.e.
is an ARMA(p,q) process, i.e.
where A(L) is a
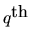 order lag-polynomial
order lag-polynomial
and B(L) is a
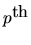 order lag-polynomial
order lag-polynomial
and the lag-operator Lk is defined by
Lk Xt = Xt-k
and
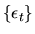 is a white-noise process,
is a white-noise process,
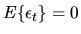 and
(cov(
and
(cov(
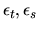 )=0 if
)=0 if 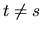 ,
,
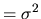 if t=s).
if t=s).
- A.
- (30%) Write down the autocovariance and
spectral density functions for this process.
- B.
- (30%) Show that if p = 0 an autoregression of Xt on
q lags of itself provides a consistent estimate of
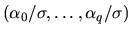 .
Is the autoregression
still consistent if p > 0?
.
Is the autoregression
still consistent if p > 0?
- C.
- (40%) Assume that a central limit
theorem holds, i.e. the distribution of
normalized sums of
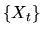 to converge in distribution to a normal random variable.
Write down an
expression for the variance of the limiting normal distribution.
to converge in distribution to a normal random variable.
Write down an
expression for the variance of the limiting normal distribution.
ANSWERS
- A.
- The answer to this question is very complicated if you
attempt to proceed via direct calculation (although it can be done),
but it much easier if you use the concept of a z-transform
and the covariance
generating function G(z) of the scalar process
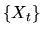 .
The answer is that spectral density function
.
The answer is that spectral density function
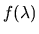 for the
for the 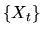 process is
given by
process is
given by
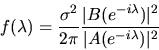 |
(29) |
provided the characteristic polynomial A(z)=0 has no roots on the
unit circle. The autocovariances of the  process can then
be derived from the spectral density via the formula
process can then
be derived from the spectral density via the formula
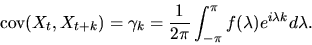 |
(30) |
Answering this question presumes a basic familiarity with Fourier
transform technology. I repeat the basics of this below.
-
- Given a sequence of real numbers
 where
k ranges from
where
k ranges from
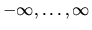 the
z-transform G(z) is defined by
the
z-transform G(z) is defined by
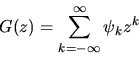 |
(31) |
where z is a complex variable satisfying
r-1 < |z| < r for some
r > 1. The autocovariance generating function is then just
the z-transform of the autocovariance sequence
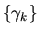 :
:
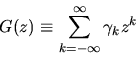 |
(32) |
where
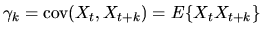 .
Thus, if we can find a representation for G(z), we can pick off
the autocovariances
.
Thus, if we can find a representation for G(z), we can pick off
the autocovariances 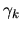 as the coefficient of zk of the
power series representation for G(z). Alternatively we can define
the spectral density
as the coefficient of zk of the
power series representation for G(z). Alternatively we can define
the spectral density
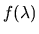 for the
for the 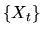 process by
process by
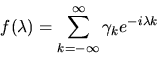 |
(33) |
where
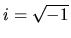 .
Note that for by the standard properties of Fourier series, we can
uncover the autocovariance
.
Note that for by the standard properties of Fourier series, we can
uncover the autocovariance 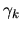 by the formula:
by the formula:
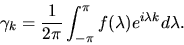 |
(34) |
This is due to the fact that the sequence of complex valued functions
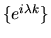 mapping
mapping
![$[-\pi,\pi]$](img113.gif) to the unit circle in the
complex plane are an orthogonal sequence under the complex
inner product for complex-valued functions mapping
to the unit circle in the
complex plane are an orthogonal sequence under the complex
inner product for complex-valued functions mapping
![$[-\pi,\pi] \to C$](img114.gif) defined by:
defined by:
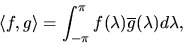 |
(35) |
where
 is the complex conjugate of
is the complex conjugate of
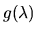 .
Since the complex conjugate of
.
Since the complex conjugate of
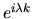 is
is
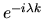 we have
we have
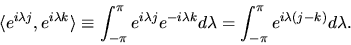 |
(36) |
Clearly if j=k then we have
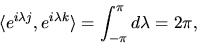 |
(37) |
but if 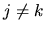 we have, using the identity
we have, using the identity
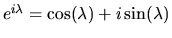 ,
,
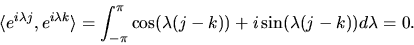 |
(38) |
since
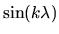 and
and
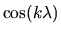 are periodic functions for
any non-zero integer k,
their integrals over the interval
are periodic functions for
any non-zero integer k,
their integrals over the interval
![$[-\pi,\pi]$](img113.gif) are zero. Thus, since
are zero. Thus, since
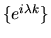 is an orthogonal family,
is an orthogonal family, 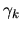 is essentially
the
is essentially
the
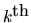 regression coefficient if we ``regress'' the
spectral density function against the sequence of orthonormal basis
functions
regression coefficient if we ``regress'' the
spectral density function against the sequence of orthonormal basis
functions
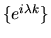 ,
,
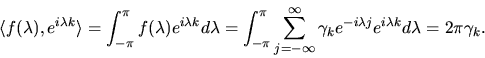 |
(39) |
Solving the above equation for 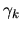 results in the Fourier
inversion formula in equation (34) above. Note also
that the spectral density is related to the covariance generating
function by the identity
results in the Fourier
inversion formula in equation (34) above. Note also
that the spectral density is related to the covariance generating
function by the identity
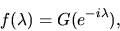 |
(40) |
so the problem reduces to finding an expression for the covariance
generating function for an
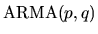 process. Assume that the
characteristic polynomial A(z) has no roots on the unit
circle, i.e. there is no complex number z with
process. Assume that the
characteristic polynomial A(z) has no roots on the unit
circle, i.e. there is no complex number z with
 such that A(z)=0. In this case it can be show (see Theorem 3.1.3 of
Brockwell and Davis, 1991), that the ARMA process
such that A(z)=0. In this case it can be show (see Theorem 3.1.3 of
Brockwell and Davis, 1991), that the ARMA process 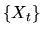 has an infinite
moving average representation:
has an infinite
moving average representation:
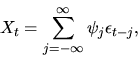 |
(41) |
where 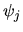 is the
is the
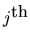 coefficient in the power series
representation of the z-transform of the
coefficient in the power series
representation of the z-transform of the
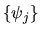 sequence,
where the z-transform
sequence,
where the z-transform 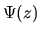 is given by
is given by
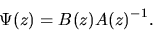 |
(42) |
However covariance generating function for an infinite MA process
(41) can be derived as follows:
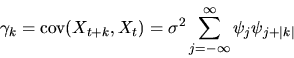 |
(43) |
Thus, the autocovariance generating function is given by
However using the fact that
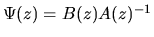 it follows that
it follows that
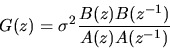 |
(45) |
Substituting
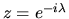 we obtain
we obtain
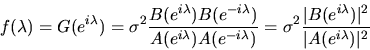 |
(46) |
since
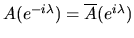 and
thus
and
thus
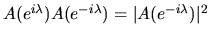 and
similarly for B.
and
similarly for B.
- B.
- When q=0 we can write the ARMA representation for
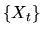 in autoregressive form:
in autoregressive form:
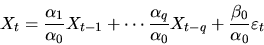 |
(47) |
Since
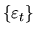 is serially uncorrelated, and since Xt-jdepends only on lagged values
is serially uncorrelated, and since Xt-jdepends only on lagged values
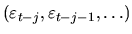 ,
it follows that
,
it follows that
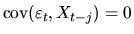 so the coefficients
so the coefficients
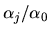 and the error variance
and the error variance
 in the above equation can be consistently estimated by
OLS. We cannot identify all the parameters unless we make an identifying
normalization on the variance of
the white noise process such as
in the above equation can be consistently estimated by
OLS. We cannot identify all the parameters unless we make an identifying
normalization on the variance of
the white noise process such as
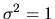 ,
or normalize
,
or normalize
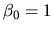 .
Suppose we make the latter normalization. Then the variance
of the estimated residuals provides a consistent estimator of
.
Suppose we make the latter normalization. Then the variance
of the estimated residuals provides a consistent estimator of
 ,
and then dividing the estimated regression coefficient
for the
,
and then dividing the estimated regression coefficient
for the
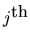 lag of Xt in the above autoregression by the
square root of the estimated variance of the
residuals provides
a consistent estimator of
lag of Xt in the above autoregression by the
square root of the estimated variance of the
residuals provides
a consistent estimator of
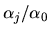 .
.
- C.
- Since
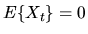 then under suitable mixing conditions
a central limit theorem will hold, i.e.
then under suitable mixing conditions
a central limit theorem will hold, i.e.
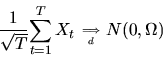 |
(48) |
where 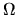 is the long run variance given by
is the long run variance given by
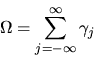 |
(49) |
where
 is the autocovariance at
lag j, which can be derived from the spectral density function
computed in part A.
is the autocovariance at
lag j, which can be derived from the spectral density function
computed in part A.
QUESTION 5 (Empirical question)
Assume that shoppers always choose only
a single
brand of canned tuna fish from the available selection of Kalternative brands of tuna fish each time they go shopping
at a supermarket. Assume initially that the (true) probability
that the decision-maker chooses brand k is the
same for everybody and is given by
 ,
,
 .
Marketing researchers
would like to learn more about these choice probabilities,
.
Marketing researchers
would like to learn more about these choice probabilities,
 and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand bi chosen by shopper i,
and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand bi chosen by shopper i,
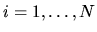 .
Thus, b1=2 denotes the observation that consumer
1 chose tuna brand 2, and b4=K denotes the observation that
consumer 4 chose tuna brand K, etc.
.
Thus, b1=2 denotes the observation that consumer
1 chose tuna brand 2, and b4=K denotes the observation that
consumer 4 chose tuna brand K, etc.
- A.
- (10%) Without doing any estimation, are there any
general
restrictions that you can place on the
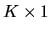 parameter
vector
parameter
vector  ?
?
-
- Answer: we must have
 and
and
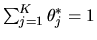 .
.
- B.
- (10%) Is it reasonable to
suppose that
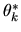 is the same for everyone? Describe
several factors that could lead different people to have different
probabilities of purchasing different brands of tuna. If you
were a consultant to Chicken of the Sea, what additional data
would you recommend that they collect in order to better predict
the probabilities that consumers buy various brands of tuna? Describe
how you would use this data once it was collected.
is the same for everyone? Describe
several factors that could lead different people to have different
probabilities of purchasing different brands of tuna. If you
were a consultant to Chicken of the Sea, what additional data
would you recommend that they collect in order to better predict
the probabilities that consumers buy various brands of tuna? Describe
how you would use this data once it was collected.
-
- Answer:
no, it is quite unreasonable to assume that everyone has the
same purchase probability. People of different ages, income levels,
ethnic backgrounds and so forth are likely to have different
tastes for tuna. Also, Chicken of the Sea is just one of many
different brands of tuna and the prices of the competing brands
and observed characteristics of the competing brands (such as whether the
tuna is packed in oil or water, the consistency of the tuna, and
other characteristics) affects the probability a given consumer
will choose Chicken of the Sea. Let the vector of observed
characteristics for the K brands be given by the
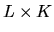 matrix
matrix
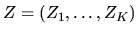 (i.e. there are L observed characteristics
for each of the K different brands).
Let the characteristics of the
(i.e. there are L observed characteristics
for each of the K different brands).
Let the characteristics of the
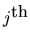 household be denoted by the
household be denoted by the
 vector Xj. Then a model
that reflects observed heterogeneity and the competing brand
characteristics would result in the following general form of the
conditional probability that household j will choose
brand k from the set of competing tuna brands offered in the
store at time of purchase,
vector Xj. Then a model
that reflects observed heterogeneity and the competing brand
characteristics would result in the following general form of the
conditional probability that household j will choose
brand k from the set of competing tuna brands offered in the
store at time of purchase,
 .
An example of a
model of consumer choice behavior that results in a
specific functional form for
.
An example of a
model of consumer choice behavior that results in a
specific functional form for
 is the
multinomial logit model. This is a model derived from a
model of utility maximization where the utility of choosing brand kis given by
is the
multinomial logit model. This is a model derived from a
model of utility maximization where the utility of choosing brand kis given by
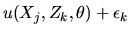 ,
where
,
where
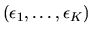 are unobserved factors affecting household j's decision, and are
assumed to have a Type III extreme value distribution. In this case,
the implied formula for
are unobserved factors affecting household j's decision, and are
assumed to have a Type III extreme value distribution. In this case,
the implied formula for
 is given by
is given by
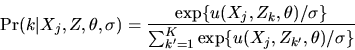 |
(50) |
where 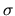 is the scale parameter in the marginal distribution of
is the scale parameter in the marginal distribution of
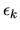 .
Thus, given data
.
Thus, given data
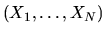 on the characteristics
of N consumers, and their choices of tuna
on the characteristics
of N consumers, and their choices of tuna
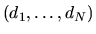 and the
observed characteristics Z, we could estimate the parameter vector
and the
observed characteristics Z, we could estimate the parameter vector
 by maximum likelihood using the log-likelihood function
by maximum likelihood using the log-likelihood function
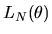 given by
given by
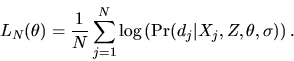 |
(51) |
and the estimated model could be used to predict how the probabilities
of purchasing different brands of tuna (and the predicted aggregate
market shares) change in response to changes in prices or observed
characteristics of the different brands of tuna.
- C.
- (20%) Using the observations
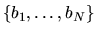 on the
observed brand choices of the sample of N shoppers, write
down an estimator for
on the
observed brand choices of the sample of N shoppers, write
down an estimator for  (under the assumption that
the ``true'' brand choice probabilities
(under the assumption that
the ``true'' brand choice probabilities  are the same
for everyone). Is your estimator unbiased?
are the same
for everyone). Is your estimator unbiased?
-
- Answer: In the simpler
case where there are no characteristics Xj or product attributes
Z, the the choice probability can be represented by a single
parameter,
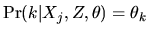 .
These
.
These 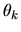 are
also the observed market shares since everyone is homogeneous.
The market share for brand k can be estimated in this
sample as the fraction of the N people
who choose brand k,
are
also the observed market shares since everyone is homogeneous.
The market share for brand k can be estimated in this
sample as the fraction of the N people
who choose brand k,
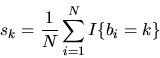 |
(52) |
Thus if sk is the observed market share for product k, then
we can estimate 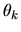 by
by
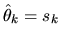 .
.
- D.
- (20%) What is the maximum likelihood estimator of
 ? Is the maximum likelihood estimator unbiased?
? Is the maximum likelihood estimator unbiased?
-
- Answer:
The likelihood function in this case can be written as
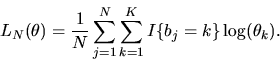 |
(53) |
subject to the constraint that
 .
Introducing a lagrange multiplier
.
Introducing a lagrange multiplier 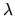 for this constraint,
the lagrangian for the likelihood function is
for this constraint,
the lagrangian for the likelihood function is
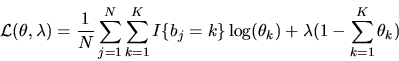 |
(54) |
The first order conditions are
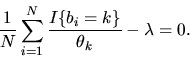 |
(55) |
Solving this for
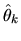 and substituting this into the
constraint, we can solve for
and substituting this into the
constraint, we can solve for 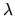 ,
obtaining
,
obtaining
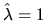 .
The
resulting estimator is the same as the intuitive market share
estimator given above, i.e.
.
The
resulting estimator is the same as the intuitive market share
estimator given above, i.e.
 |
(56) |
If the data
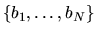 are really IID
and the ``representative consumer'' model is really correct, then
are really IID
and the ``representative consumer'' model is really correct, then
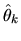 is an unbiased estimator of
is an unbiased estimator of
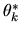 since
since
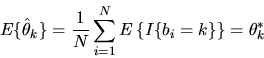 |
(57) |
since the random variable
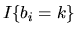 is a bernoulli random variable
which equals 1 with probability
is a bernoulli random variable
which equals 1 with probability
 and 0 with probability
and 0 with probability
 .
.
- E.
- (40%) Suppose Chicken of the Sea Tuna company
also collected data on the prices
 that the supermarket charged for each
of the K different brands of tuna fish. Suppose someone proposed
that the probability of buying brand j was a function of
the prices of all the various brands of tuna,
that the supermarket charged for each
of the K different brands of tuna fish. Suppose someone proposed
that the probability of buying brand j was a function of
the prices of all the various brands of tuna,
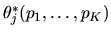 ,
given by:
,
given by:
Describe in general terms
how to estimate the parameters
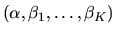 .
If
.
If 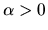 ,
does an increase
in pj decrease or increase the probability that a shopper would buy
brand j?
,
does an increase
in pj decrease or increase the probability that a shopper would buy
brand j?
-
- Answer: This answer was already discussed in
the answer to part B. The model is a special case of the more
general multinomial logit model discussed in the answer to part B. In
this case the implicit utility function only depends on the single
characteristic of brand k, namely its price pk and the other
characteristics of the brand are implicitly captured in the brand-specific
dummy variable
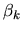 .
Since now consumer-level characteristics
enter the model, the utility function is given by
.
Since now consumer-level characteristics
enter the model, the utility function is given by
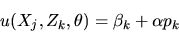 |
(58) |
where
 .
If
.
If
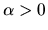 then
the utility of brand k increases in the price of the brand k,
an economically counter-intuitive result. This sugggests that the
probability of purchasing brand k is an increasing function
of pk and this can be verified by computing
then
the utility of brand k increases in the price of the brand k,
an economically counter-intuitive result. This sugggests that the
probability of purchasing brand k is an increasing function
of pk and this can be verified by computing
![\begin{displaymath}{ \partial \mbox{Pr} \over \partial p_K}
(k\vert p_1,\ldots,...
..._K,\theta) [1 -
\mbox{Pr}(k\vert p_1,\ldots,p_K,\theta)] > 0.
\end{displaymath}](img209.gif) |
(59) |
QUESTION 6 (Regression question)
Let (yt,xt) be IID observations from a regression model
where yt, xt, and
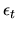 are all
scalars. Suppose that
are all
scalars. Suppose that
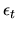 is normally
distributed with
is normally
distributed with
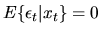 ,
but
,
but
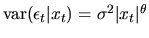 .
Consider the following two estimators for
.
Consider the following two estimators for
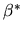 :
:
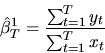

- A.
- (20%) Are these two estimators consistent estimators of
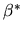 ? Which estimator is more efficient when:
1) if we know a priori that
? Which estimator is more efficient when:
1) if we know a priori that
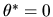 ,
and 2) we don't know
,
and 2) we don't know  ?
Explain your reasoning for full credit.
?
Explain your reasoning for full credit.
-
- Answer: Both estimators are consistent
estimators of
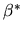 .
To see this note that by dividing the
numerator and denominator of
.
To see this note that by dividing the
numerator and denominator of
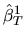 and applying the Law of
Large Numbers we obtain
and applying the Law of
Large Numbers we obtain
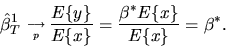 |
(60) |
The second estimator is the OLS estimator and it is also a consistent
estimator of 
 |
(61) |
When
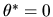 the Gauss-Markov Theorem applies and the OLS
estimator is the best linear unbiased estimator of
the Gauss-Markov Theorem applies and the OLS
estimator is the best linear unbiased estimator of 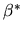 .
It is
also the maximum likelihood estimator when the errors are
normally distributed, and so is asymptotically
efficient in the class of all (potentially nonlinear) regular estimators
of
.
It is
also the maximum likelihood estimator when the errors are
normally distributed, and so is asymptotically
efficient in the class of all (potentially nonlinear) regular estimators
of 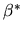 .
We can derive the asymptotic efficiency of
.
We can derive the asymptotic efficiency of
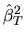 relative to
relative to
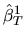 through a simple application of the central
limit theorem. We have
through a simple application of the central
limit theorem. We have
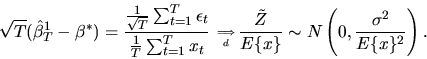 |
(62) |
where
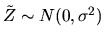 .
Similarly, the asymptotic
distribution of the OLS estimator
.
Similarly, the asymptotic
distribution of the OLS estimator
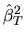 is given by
is given by
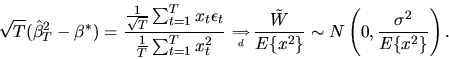 |
(63) |
where
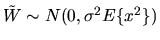 .
If the variance of
.
If the variance of 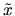 is positive we have
is positive we have
This implies that the asymptotic variance of
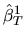 is
greater than the asymptotic variance of
is
greater than the asymptotic variance of
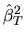 .
.
-
- In the case where we don't know
 we can
repeat the calculations given above, but the asymptotic distributions
of the two estimators will depend on the unknown parameter
we can
repeat the calculations given above, but the asymptotic distributions
of the two estimators will depend on the unknown parameter  .
In particular, when
.
In particular, when
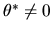 the unconditional variance of
the unconditional variance of
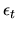 is given by
is given by
 |
(65) |
This implies that
![\begin{displaymath}\sqrt{T}(\hat\beta^1_T - \beta^*) = { { 1 \over \sqrt{T}} \su...
...igma^2
E\{\vert x\vert^{\theta^*}\} \over [E\{x\}]^2} \right).
\end{displaymath}](img232.gif) |
(66) |
since with heteroscedasticity, the random variable
 ,
the asymptotic distribution of
,
the asymptotic distribution of
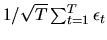 ,
is
,
is
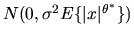 instead of
instead of
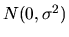 .
Similarly we have
.
Similarly we have
![\begin{displaymath}\sqrt{T}(\hat\beta^2_T - \beta^*) = { { 1 \over \sqrt{T}} \su...
...E\{ x^2
\vert x\vert^{\theta^*}\} \over
[E\{x^2\}]^2} \right).
\end{displaymath}](img236.gif) |
(67) |
In this case, which of the two estimators
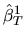 or
or
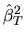 is more efficient depends on the value of
is more efficient depends on the value of  .
.
- B.
- (20%) Write down an asymptotically
optimal estimator for
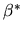 if we know the value of
if we know the value of  a priori.
a priori.
-
- Answer:
If we know
 we can do maximum likelihood
using the conditional density of y given x given by
we can do maximum likelihood
using the conditional density of y given x given by
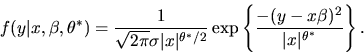 |
(68) |
The maximum likeihood estimator in this case can be easily shown to
be a form of weighted least squares:
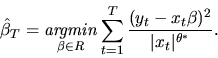 |
(69) |
- C.
- (20%) Write down an asymptotically optimal estimator for
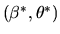 if we don't know the value of
if we don't know the value of  a
priori.
a
priori.
-
- Answer: If we don't know
 a
priori we can still use the likelihood function given in part B
to estimate
a
priori we can still use the likelihood function given in part B
to estimate
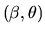 jointly. The maximum likelihood estimator
for
jointly. The maximum likelihood estimator
for  can also be cast as a weighted least squares estimator,
but in the case where
can also be cast as a weighted least squares estimator,
but in the case where  is not known we replace
is not known we replace  in formula (69) by
in formula (69) by
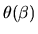 ,
where this is the unique
solution to
,
where this is the unique
solution to
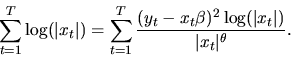 |
(70) |
The maximum likelihood estimator for  is then given by
is then given by
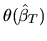 where
where
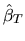 is the weighted least
squares estimator given above.
is the weighted least
squares estimator given above.
- D.
- (20%) Describe the feasible GLS estimator for
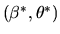 .
Is the feasible GLS estimator asymptotically efficient?
.
Is the feasible GLS estimator asymptotically efficient?
-
- Answer: The feasible GLS estimator is based on
an initial inefficient estimator
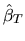 of
of 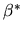 which is used to construct
estimated residuals
which is used to construct
estimated residuals
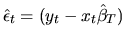 and from
these
an estimator for
and from
these
an estimator for  .
If we could observe the true residuals we
could estimate
.
If we could observe the true residuals we
could estimate  via the following
nonlinear regression of
via the following
nonlinear regression of
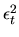 on xt
on xt
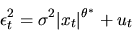 |
(71) |
where
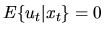 .
This suggests that it should be possible to
estimate
.
This suggests that it should be possible to
estimate  using the estimated residuals
using the estimated residuals
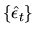 as follows
as follows
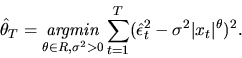 |
(72) |
It can be shown that if the initial estimator
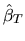 is
is
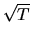 -consistent, then the nonlinear least squares estimator for
-consistent, then the nonlinear least squares estimator for
 given above will also be
given above will also be 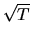 -consistent, and that the
following three step, feasible GLS estimator for
-consistent, and that the
following three step, feasible GLS estimator for 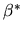 will be
asymptotically efficient:
will be
asymptotically efficient:
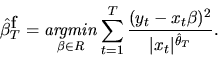 |
(73) |
- E.
- (20%) How would your answers to parts A to D change
if you didn't know the distribution of
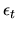 was normal?
was normal?
-
- Answer: The answer to part A is unchanged.
However if we don't know the form of the conditional
distribution of
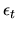 given xt, we can't write down
a likelihood function that will determine the asymptotically
optimal estimator for
given xt, we can't write down
a likelihood function that will determine the asymptotically
optimal estimator for 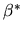 ,
regardless of whether we know
,
regardless of whether we know
 or not. Thus, there is no immediate answer to parts
B and C. In part D we can still do the same feasible GLS estimator,
and while it is possible to show that this is asymptotically
efficient relative to OLS, it is not clear that it is asymptotically
optimal. There is a possibility of doing adaptive estimation,
i.e. of using a first stage inefficient estimator of
or not. Thus, there is no immediate answer to parts
B and C. In part D we can still do the same feasible GLS estimator,
and while it is possible to show that this is asymptotically
efficient relative to OLS, it is not clear that it is asymptotically
optimal. There is a possibility of doing adaptive estimation,
i.e. of using a first stage inefficient estimator of 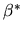 to
construct estimated residuals
to
construct estimated residuals
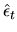 and then using these
estimated residuals to try to estimate the conditional density
and then using these
estimated residuals to try to estimate the conditional density
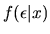 non-parametrically. Then using this nonparamtric
distribution we could do maximum likelihood. Unfortunately the known results
for this sort of adaptive estimation procedure requires that
the error term
non-parametrically. Then using this nonparamtric
distribution we could do maximum likelihood. Unfortunately the known results
for this sort of adaptive estimation procedure requires that
the error term
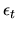 be independent of xt. However if there
is heteroscedasticity, then
be independent of xt. However if there
is heteroscedasticity, then
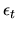 will not be independent of
xt and adaptive estimation may not be possible. In this case
the most efficient possible estimator can be ascertained by
deriving the semi-parametric efficiency bound for the
parameter of interest
will not be independent of
xt and adaptive estimation may not be possible. In this case
the most efficient possible estimator can be ascertained by
deriving the semi-parametric efficiency bound for the
parameter of interest  ,
where the conditional density
,
where the conditional density
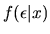 is treated as a non-parametric ``nuisance parameter''.
However this goes far beyond what I expected students to write in the
answer to this exam.
is treated as a non-parametric ``nuisance parameter''.
However this goes far beyond what I expected students to write in the
answer to this exam.
Part III (60 minutes, 55 points). Do 1 out of the
4 questions below.
QUESTION 1 (Hypothesis testing) Consider the GMM estimator with IID data, i.e
the observations
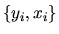 are independent and identically distributed
using the moment condition
are independent and identically distributed
using the moment condition
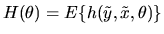 ,
where h is a
,
where h is a
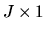 vector of moment conditions and
vector of moment conditions and
 is a
is a
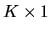 vector of parameters to be estimated.
Assume that the moment conditions are correctly specified, i.e. assume there
is a unique
vector of parameters to be estimated.
Assume that the moment conditions are correctly specified, i.e. assume there
is a unique  such that
such that
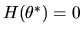 .
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically
.
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically 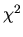 with
J-K degrees of freedom:
with
J-K degrees of freedom:
![\begin{displaymath}N H_N(\hat\theta_N)' [\hat\Omega_N]^{-1}
H_N(\hat\theta_N)_{\Longrightarrow \atop d} \chi^2(J-K),
\end{displaymath}](img259.gif) |
(74) |
where HN is a
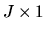 vector of moment conditions,
vector of moment conditions,  is a
is a
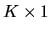 vector of parameters,
vector of parameters,
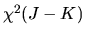 is a Chi-squared random variable with J-K degrees of freedom,
is a Chi-squared random variable with J-K degrees of freedom,
and
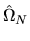 is a consistent estimator of
is a consistent estimator of 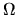 given by
given by
Hint: Use Taylor series expansions to provide
a formula for
 from the first order
condition for
from the first order
condition for
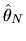
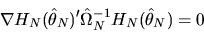 |
(75) |
and a Taylor series expansion of
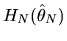 about
about 
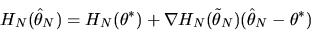 |
(76) |
where
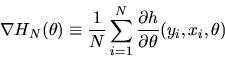 |
(77) |
is the
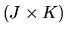 matrix of partial derivatives of the moment
conditions
matrix of partial derivatives of the moment
conditions
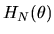 with respect to
with respect to  and
and
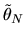 is a vector each of whose elements are on the line segment joining the
corresponding components of
is a vector each of whose elements are on the line segment joining the
corresponding components of
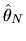 and
and  .
Use the above
two equations to derive the following formula for
.
Use the above
two equations to derive the following formula for
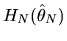
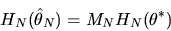 |
(78) |
where
![\begin{displaymath}M_N= \left[ I - \nabla H_N(\hat\theta_N)[\nabla H_N(\hat\thet...
...N)]^{-1} \nabla
H_N(\hat\theta_N)' \hat\Omega^{-1}_N \right].
\end{displaymath}](img274.gif) |
(79) |
Show that with probability 1 we have 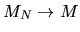 where M is a
where M is a
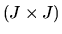 idempotent matrix. Then using this result, and using
the Central Limit Theorem to show that
idempotent matrix. Then using this result, and using
the Central Limit Theorem to show that
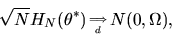 |
(80) |
and using the probability result from Question 0 of Part II,
show that the minimized value of the GMM criterion function
does indeed converge in distribution to a
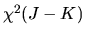 random
variable as claimed in equation (74).
random
variable as claimed in equation (74).
ANSWER: The hint provides most of the answer.
Plugging the Taylor series expansion for
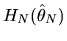 given in equation (76) into the GMM first order
condition given in equation (75) and solving
for
given in equation (76) into the GMM first order
condition given in equation (75) and solving
for
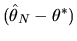 we obtain
we obtain
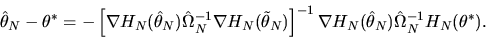 |
(81) |
Substituting the above expression for
 back into the Taylor series expansion for
back into the Taylor series expansion for
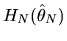 in
equation (76) we obtain the representation for
in
equation (76) we obtain the representation for
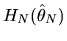 given in equations (78) and
(79). Now we can write the optimized value
of the GMM objective function as
given in equations (78) and
(79). Now we can write the optimized value
of the GMM objective function as
Now, since
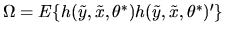 ,
it follows from the Central Limit Theorem that
,
it follows from the Central Limit Theorem that
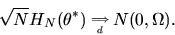 |
(83) |
so that
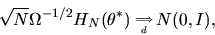 |
(84) |
where I is the
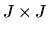 identity matrix. Now consider the matrix
in the middle of the expansion of the quadratic form in equation
(82). We have
identity matrix. Now consider the matrix
in the middle of the expansion of the quadratic form in equation
(82). We have
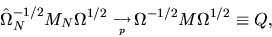 |
(85) |
where
![\begin{displaymath}Q = \left[I - \Omega^{-1/2} \nabla H(\theta^*)[\nabla H(\thet...
...la
H(\theta^*)]^{-1} \nabla H(\theta^*)' \Omega^{-1/2}\right],
\end{displaymath}](img289.gif) |
(86) |
and where
![\begin{displaymath}M = \left[I - \nabla H(\theta^*)[\nabla H(\theta^*)'\Omega^{-...
...abla
H(\theta^*)]^{-1} \nabla H(\theta^*)' \Omega^{-1}\right],
\end{displaymath}](img290.gif) |
(87) |
and where
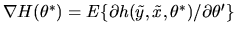 .
It is straightfoward to verify that the matrix Q in equation
(86) is symmetric and idempotent. Thus, we have
.
It is straightfoward to verify that the matrix Q in equation
(86) is symmetric and idempotent. Thus, we have
![\begin{displaymath}N H_N(\hat\theta_N)' [\hat\Omega^{-1}_N]^{-1}
H_N(\hat\theta_...
...ow \atop d} [Q \tilde Z]' [Q
\tilde Z] = \tilde Z' Q \tilde Z,
\end{displaymath}](img292.gif) |
(88) |
where
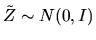 .
By the probability result in Question 1 of
Part II, it follows that
.
By the probability result in Question 1 of
Part II, it follows that
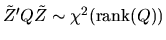 .
However we have
.
However we have
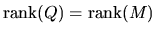 ,
and
,
and
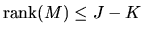 due to
the fact that
due to
the fact that
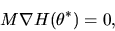 |
(89) |
where 0 denotes a
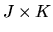 matrix of zeros, as can be
verified by multiplying
matrix of zeros, as can be
verified by multiplying
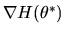 on both sides of equation
(87). However since Q = I - R where R is given by
on both sides of equation
(87). However since Q = I - R where R is given by
![\begin{displaymath}R= \Omega^{-1/2} \nabla H(\theta^*)[\nabla H(\theta^*)'\Omega^{-1}\nabla
H(\theta^*)]^{-1} \nabla H(\theta^*)' \Omega^{-1/2}
\end{displaymath}](img300.gif) |
(90) |
and
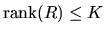 ,
it follows that
,
it follows that
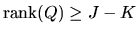 .
Combining these two inequalities we have
.
Combining these two inequalities we have
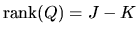 and we
conclude that we have established the result tat
and we
conclude that we have established the result tat
 |
(91) |
QUESTION 2 (Consistency of Bayesian posterior)
Consider a Bayesian who has observes
IID data
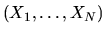 ,
where
,
where
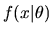 is the likelihood for a single observation,
and
is the likelihood for a single observation,
and 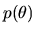 is the prior density
over
an unknown finite-dimensional parameter
is the prior density
over
an unknown finite-dimensional parameter
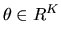 .
.
- A.
- (10%) Use Bayes Rule to derive a formula for the
posterior density of
 given
given
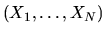 .
.
-
- Answer: The posterior is given by
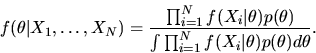 |
(92) |
- B.
- (20%) Let
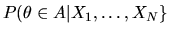 be the posterior probability
be the posterior probability
 is in some set
is in some set
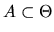 given the first
N observations. Show that this posterior probability
satisfies the Law of iterated expectations:
given the first
N observations. Show that this posterior probability
satisfies the Law of iterated expectations:
-
- Answer: The formula for the
posterior probability that
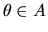 given
given
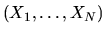 is
just the expectation of the indicator function
is
just the expectation of the indicator function
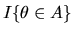 with
respect to the posterior density for
with
respect to the posterior density for  given above. That is,
given above. That is,
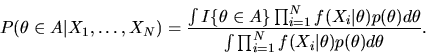 |
(93) |
Similarly, we have
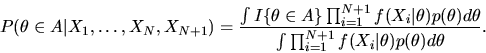 |
(94) |
Now, to compute the conditional expectation
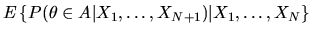 we note that the
appropriate density to use is our posterior belief about XN+1 given
we note that the
appropriate density to use is our posterior belief about XN+1 given
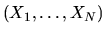 .
This conditional density can be derived using the
posterior for
.
This conditional density can be derived using the
posterior for 
Thus,
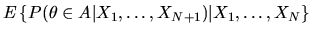 is given by
is given by
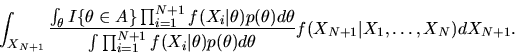 |
(96) |
Using the formula for
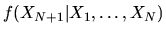 given in
equation (95) we get
given in
equation (95) we get
- C.
- (20%) A martingale
is a stochastic process
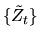 that satisfies
that satisfies
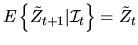 ,
where
,
where
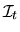 denotes the information set at time t and
includes knowledge of all past Zt's up to time t,
denotes the information set at time t and
includes knowledge of all past Zt's up to time t,
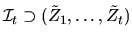 .
Use the
result in part A to show that the process
.
Use the
result in part A to show that the process
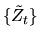 where
where
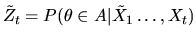 is a
martingale. (We are interested in martingales because
the Martingale Convergence Theorem can be used to show that
if
is a
martingale. (We are interested in martingales because
the Martingale Convergence Theorem can be used to show that
if  is finite-dimensional, then the posterior
distribution converges with probability 1 to a point mass on the
true value of
is finite-dimensional, then the posterior
distribution converges with probability 1 to a point mass on the
true value of  generating the observations
generating the observations 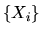 .
But
you don't have to know anything about this to answer this question.)
.
But
you don't have to know anything about this to answer this question.)
-
- The Law of the Iterated Expectations argument
above is the proof that the
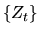 process,
process,
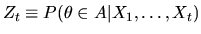 ,
is a martingale. That is,
if we let
,
is a martingale. That is,
if we let
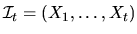 ,
then
we have
,
then
we have
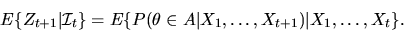 |
(98) |
The Law of Iterated Expectations result above establishes that
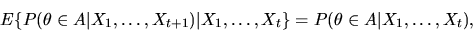 |
(99) |
from which we conclude that the posterior probability process
is a martingale.
- D.
- (50%) Suppose that if
 is restricted to the
K-dimensional
simplex,
is restricted to the
K-dimensional
simplex,
 with
with
 ,
,
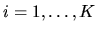 ,
,
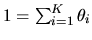 ,
and the distribution
of Xi given
,
and the distribution
of Xi given  is multinomial with parameter
is multinomial with parameter  ,
i.e.
,
i.e.
Suppose the prior distribution over  ,
,
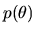 is Dirichlet with parameter
is Dirichlet with parameter 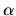 :
:
where both
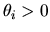 and
and
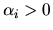 ,
,
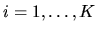 .
Compute
the posterior distribution and show 1) the posterior is also
Dirichlet (i.e. the Dirichlet is a conjugate family),
and show directly that
as
.
Compute
the posterior distribution and show 1) the posterior is also
Dirichlet (i.e. the Dirichlet is a conjugate family),
and show directly that
as
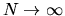 that the posterior distribution converges to
a point mass on the true parameter
that the posterior distribution converges to
a point mass on the true parameter  generating the data.
generating the data.
Answer: The Dirichlet-Multinomial combination is a
conjugate family of distributions. That is, if the prior
distribution is Dirichlet with prior hyperparameters
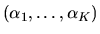 and the data are generated by a multinomial
with K mutually exclusive outcomes, then the posterior distribution
after observing N IID draws from the multinomial
is also Dirichlet with parameter
and the data are generated by a multinomial
with K mutually exclusive outcomes, then the posterior distribution
after observing N IID draws from the multinomial
is also Dirichlet with parameter
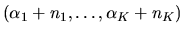 where
where
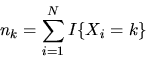 |
(100) |
By the Law of Large Numbers we have that
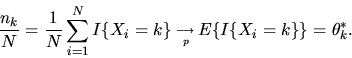 |
(101) |
We prove the consistency of the posterior by showing that for
any
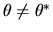 we have with probability 1
we have with probability 1
 |
(102) |
This implies that the limiting posterior puts infinitely more weight
on the event that
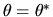 than on any other possible value
for
than on any other possible value
for  .
Dividing by N and taking limits we have
.
Dividing by N and taking limits we have
![\begin{displaymath}\lim_{N \to \infty} { 1\over N} \log\left({ p(\theta^*\vert X...
...^K
\theta^*_k \left[ \log(\theta^*_k) - \log(\theta_k)\right].
\end{displaymath}](img357.gif) |
(103) |
However by the Information Inequality we have
![\begin{displaymath}\sum_{k=1}^K
\theta^*_k \left[ \log(\theta^*_k) - \log(\theta_k)\right] > 0.
\end{displaymath}](img358.gif) |
(104) |
This result implies that with probability 1
![\begin{displaymath}\lim_{N \to \infty} \log\left({ p(\theta^*\vert X_1,\ldots,X_...
...a\vert X_1,\ldots,X_N)} \right)\right] \longrightarrow \infty, \end{displaymath}](img359.gif) |
(105) |
since the latter term converges with probability 1 to a positive
quantity.
Another way to see the result is to note that if
the
 vector
vector
 has a Dirichlet distribution
with
parameter
has a Dirichlet distribution
with
parameter
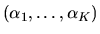 then
then
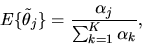 |
(106) |
and
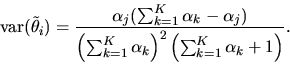 |
(107) |
Since the posterior distribution is Dirichlet with parameter
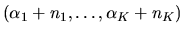 ,
we can divide the numerator
and denominator of the expression for
,
we can divide the numerator
and denominator of the expression for
 by N and use the Law of Large Numbers to show that in the limit
with probability 1 we have
by N and use the Law of Large Numbers to show that in the limit
with probability 1 we have
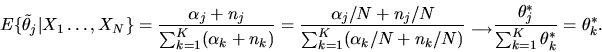 |
(108) |
Via a similar sort of calculation, we can show that the
conditional variance
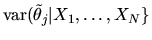 converges to zero since we have
converges to zero since we have
and the numerator of the latter expression converges with
probability 1 to
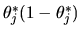 but the denominator
converges to
but the denominator
converges to 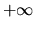 with probability 1.
with probability 1.
QUESTION 3
Consider the random utility model:
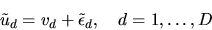 |
(110) |
where
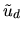 is a decision-maker's payoff or utility for selecting
alternative d from a set containing D possible alternatives (we
assume that the individual only chooses one item). The term vd is
known as the deterministic or strict utility from alternative
d and the error term
is a decision-maker's payoff or utility for selecting
alternative d from a set containing D possible alternatives (we
assume that the individual only chooses one item). The term vd is
known as the deterministic or strict utility from alternative
d and the error term
 is the random component of
utility. In empirical applications vd is often specified as
is the random component of
utility. In empirical applications vd is often specified as
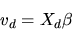 |
(111) |
where Xd is a vector of observed covariates and  is a vector
of coefficients determining the agent's utility to be estimated. The
interpretation is that Xd represents a vector of characteristics
of the decision-maker and alternative d that are observable
by the econometrician and
is a vector
of coefficients determining the agent's utility to be estimated. The
interpretation is that Xd represents a vector of characteristics
of the decision-maker and alternative d that are observable
by the econometrician and
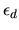 represents characteristics
of the agent and alternative d that affect the utility of choosing
alternative d which are unobserved by the econometrician. Define
the agent's decision rule
represents characteristics
of the agent and alternative d that affect the utility of choosing
alternative d which are unobserved by the econometrician. Define
the agent's decision rule
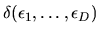 by:
by:
![\begin{displaymath}\delta(\epsilon) = \mbox{\it argmax\/}_{d=1,\ldots,D} \left[ v_d +
\tilde \epsilon_d\right] \end{displaymath}](img377.gif) |
(112) |
i.e.
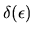 is the optimal choice for an agent whose
unobserved utility components are
is the optimal choice for an agent whose
unobserved utility components are
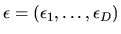 .
Then the agent's choice
probability
.
Then the agent's choice
probability 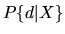 is given by:
is given by:
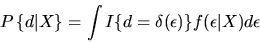 |
(113) |
where
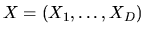 is the vector of observed characteristics of
the agent and the D alternatives and
is the vector of observed characteristics of
the agent and the D alternatives and
 is the
conditional density function of the random components of utility given
the values of observed components X, and
is the
conditional density function of the random components of utility given
the values of observed components X, and
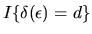 is the indicator function given by
is the indicator function given by
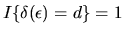 if
if
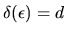 and 0 otherwise.
Note that the integral above is
actually a multivariate integral over the D components of
and 0 otherwise.
Note that the integral above is
actually a multivariate integral over the D components of
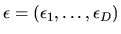 ,
and simply represents the
probability that the values of the vector of unobserved utilities
,
and simply represents the
probability that the values of the vector of unobserved utilities 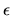 lead the agent to choose alternative d.
lead the agent to choose alternative d.
Definition: The Social Surplus Function
 is given by:
is given by:
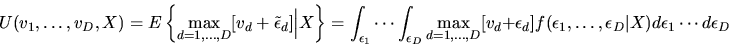 |
(114) |
The Social Surplus function is the expected maximized utility of the
agent.1
- A.
- (50%) Prove the Williams-Daly-Zachary Theorem:
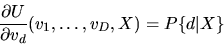 |
(115) |
and discuss its relationship to Roy's Identity.
-
- Hint: Interchange the differentiation and expectation
operations when computing
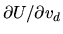 :
:
and show that
-
- Answer: The hint gives away most of the
answer. We simply appeal to the Lebesgue Dominated Convergence Theorem
to justify the interchange of integration and differentiation operators.
As long as the distribution of the
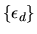 's has a density,
the derivative
's has a density,
the derivative
![\begin{displaymath}\partial/\partial v_d \max_{d=1,\ldots,D}[v_d +
\epsilon_d] = I\{d = \delta(\epsilon)\}.
\end{displaymath}](img394.gif) |
(116) |
exists almost everywhere with respect to this
density and is bounded by 1, so that the Lebesgue Dominated
Convergence Theorem applies. It is easy to see why the partial derivative
of
![$\max_{d=1,\ldots,D}[v_d + \epsilon_d]$](img395.gif) equals the indicator
function
equals the indicator
function
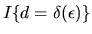 :
if this function equals 1then alternative d yields the highest utility and we have
:
if this function equals 1then alternative d yields the highest utility and we have
Thus,
![$v_d + \epsilon_d = \max_{d'=1,\ldots,D}[v_{d'} +
\epsilon_{d'}]$](img398.gif) and we have
and we have
![$\partial /\partial v_d
\max_{d=1,\ldots,D}[v_d +
\epsilon_d] =1 $](img399.gif) when
when
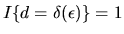 .
However when
.
However when
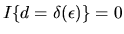 ,
then alternative d is not the utility
maximizing choice, so that
,
then alternative d is not the utility
maximizing choice, so that
![$\max_{d'=1,\ldots,D}[v_{d'} +
\epsilon_{d'}] > v_d + \epsilon_d$](img402.gif) .
It follows that
we have
.
It follows that
we have
![$\partial /\partial v_d
\max_{d=1,\ldots,D}[v_d +
\epsilon_d] =0 $](img403.gif) when
when
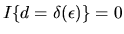 so that the identity
claimed in (116) holds with probability 1, and so via
the Lebesgue Dominated Convergence Theorem we have
so that the identity
claimed in (116) holds with probability 1, and so via
the Lebesgue Dominated Convergence Theorem we have
- B.
- (50%) Consider the special case of
the random utility model when
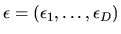 has a multivariate (Type I) extreme value distribution:
has a multivariate (Type I) extreme value distribution:
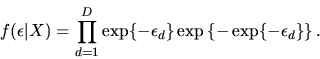 |
(118) |
Show that the conditional choice probability 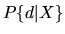 is given by
the multinomial logit formula:
is given by
the multinomial logit formula:
 |
(119) |
Hint 1: Use the Williams-Daly-Zachary Theorem, showing
that in the case of the extreme value distribution (118) the Social
Surplus function is given by
![\begin{displaymath}U(v_1,\ldots,v_D,X)= \sigma\gamma+ \sigma\log\left[
\sum_{d=1}^D \exp\{ v_d/\sigma\} \right].
\end{displaymath}](img411.gif) |
(120) |
where
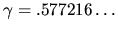 is Euler's constant.
is Euler's constant.
Hint 2: To derive equation (120) show that the
extreme value family is max-stable: i.e. if
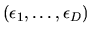 are IID extreme value random variables, then
are IID extreme value random variables, then
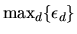 also has an extreme value distribution. Also
use the fact that the expectation of a single extreme value random
variable with location parameter
also has an extreme value distribution. Also
use the fact that the expectation of a single extreme value random
variable with location parameter 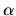 and scale parameter
and scale parameter
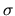 is given by:
is given by:
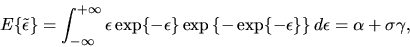 |
(121) |
and the CDF is given by
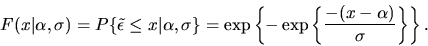 |
(122) |
Hint 3: Let
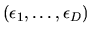 be
INID (independent, non-identically distributed) extreme value
random variables with location parameters
be
INID (independent, non-identically distributed) extreme value
random variables with location parameters
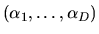 and common scale parameter
and common scale parameter 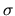 .
Show that this family is
max-stable by proving that
.
Show that this family is
max-stable by proving that
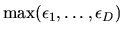 is an extreme
value random variable with scale parameter
is an extreme
value random variable with scale parameter 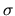 and location parameter
and location parameter
![\begin{displaymath}\alpha = \sigma \log\left[ \sum_{d=1}^D \exp\{ \alpha_d/\sigma\}
\right]
\end{displaymath}](img419.gif) |
(123) |
-
- Answer: Once again, the hints are virtually
the entire answer to the problem. By hint 1, if the Social Surplus
function is given by equation (120) then by the
Williams-Daly-Zachary Theorem we have
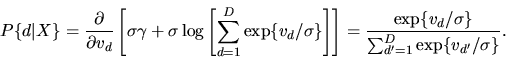 |
(124) |
-
- Now to show that the Social Surplus function has
the form given in equation (120), we use the fact that
if
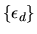 are independent random variables, we have
following formula
for the probability distribution of the random variable
are independent random variables, we have
following formula
for the probability distribution of the random variable
![$\max_{d=1,\ldots,D}[v_d + \epsilon_d]$](img395.gif) :
:
![\begin{displaymath}\mbox{Pr}\left\{ \max_{d=1,\ldots,D}[v_d + \epsilon_d] \le x\...
...\prod_{d=1}^D \mbox{Pr}\left\{ v_d + \epsilon_d \le x\right\}.
\end{displaymath}](img421.gif) |
(125) |
Now, let
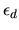 have a Type III extreme value
value distribution with location parameter
have a Type III extreme value
value distribution with location parameter
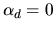 and scale
parameter
and scale
parameter
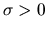 .
Then it is easy to see that
.
Then it is easy to see that
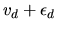 is also a Type III extreme value random variate with location parameter
vd and scale parameter
is also a Type III extreme value random variate with location parameter
vd and scale parameter 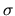 .
That is, the family of independent
Type III extreme distributions is max-stable. Plugging in the formula for
the Type III extreme value distribution from equation
(122) into the formula for the CDF of
.
That is, the family of independent
Type III extreme distributions is max-stable. Plugging in the formula for
the Type III extreme value distribution from equation
(122) into the formula for the CDF of
![$\max_{d=1,\ldots,D}[v_d + \epsilon_d]$](img395.gif) given above, we find that
given above, we find that
![\begin{displaymath}\mbox{Pr}\left\{ \max_{d=1,\ldots,D}[v_d + \epsilon_d] \le x\...
...ft\{ - \exp\left\{ {-(x-\alpha) \over \sigma}\right\}\right\},
\end{displaymath}](img425.gif) |
(126) |
where the location parameter is given by the log-sum formula
in equation (123). The form of the
Social Surplus Function in equation (120) then follows from
the formula for the expectation of an extreme value random variate
in equation (121), and formula (123) for the
location parameter of the maximum of a collection of independent
Type III extreme random variables, i.e.
![\begin{displaymath}U(v_1,\ldots,v_D,X) \equiv E\left\{ \max_{d=1,\ldots,D}[v_d +...
...a+ \sigma\log\left[
\sum_{d=1}^D \exp\{ v_d/\sigma\} \right].
\end{displaymath}](img426.gif) |
(127) |
QUESTION 4 (Latent Variable Models) The Binary
Probit Model can be viewed as a simple type of latent variable
model. There is an underlying linear regression model
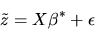 |
(128) |
but where the dependent variable  is latent, i.e.
it is not observed by the econometrician. Instead we observe the
dependent variable y given by
is latent, i.e.
it is not observed by the econometrician. Instead we observe the
dependent variable y given by
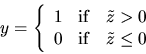 |
(129) |
- 1.
- (5%) Assume that the error term
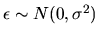 .
Show
that the scale of
.
Show
that the scale of 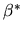 and the
parameter
and the
parameter 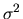 is not simultaneously identified and therefore without
loss of generality we can normalize
is not simultaneously identified and therefore without
loss of generality we can normalize
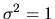 and interpret the
estimated
and interpret the
estimated  coefficients as being the true coefficients
coefficients as being the true coefficients 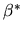 divided by
divided by 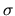 :
:
 |
(130) |
-
- Answer: Notice that if
 is an
arbitrary positive constant, then if we divide both sides of equation
(128) by
is an
arbitrary positive constant, then if we divide both sides of equation
(128) by 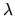 ,
the probability distribution for the
observed dependent variable has not changed since we have
,
the probability distribution for the
observed dependent variable has not changed since we have
 |
(131) |
Thus the model with latent variable
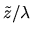 is
observationally equivalent to the model with the latent
variable
is
observationally equivalent to the model with the latent
variable  .
If we normalize the variance of
.
If we normalize the variance of 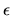 to 1,
this is equivalent to dividing
to 1,
this is equivalent to dividing  by the standard deviation
by the standard deviation
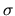 of the underlying ``true''
of the underlying ``true'' 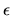 variable, so that
our estimates of
variable, so that
our estimates of  should be interpreted as being estimates
of
should be interpreted as being estimates
of
 .
.
- 2.
- (10%) Derive the conditional probability
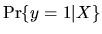 in terms of X,
in terms of X,  and the standard normal CDF,
and the standard normal CDF,  and use
this probability to write down the likelihood function for NIID observations of pairs
and use
this probability to write down the likelihood function for NIID observations of pairs
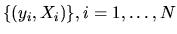 .
.
-
- Answer: We have
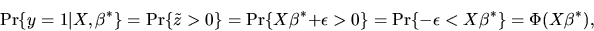 |
(132) |
where  is the CDF of a N(0,1) random variable, and we used the
fact that if
is the CDF of a N(0,1) random variable, and we used the
fact that if
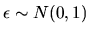 then
then
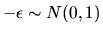 .
Using
this formula, the likelihood for N observations
.
Using
this formula, the likelihood for N observations
 is
given by
is
given by
![\begin{displaymath}L(\beta) = \prod_{i=1}^N [\Phi(X_i\beta)]^{y_i}
[1-\Phi(X_i\beta)]^{(1-y_i)}. \end{displaymath}](img442.gif) |
(133) |
- 3.
- (20%) Show that
 can
be consistently estimated by nonlinear
least squares by writing down the least squares problem and
sketching a proof for its consistency.
can
be consistently estimated by nonlinear
least squares by writing down the least squares problem and
sketching a proof for its consistency.
-
- We observe that y satisfies the following
nonlinear regression equation:
 |
(134) |
where
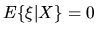 .
To see this, note that conditional on
X the residual
.
To see this, note that conditional on
X the residual  takes on two possible values. If y=1, which
occurs with probability
takes on two possible values. If y=1, which
occurs with probability
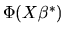 ,
then
,
then
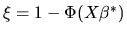 .
If y=0, which occurs with probability
.
If y=0, which occurs with probability
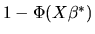 ,
then
,
then
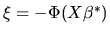 .
Thus we have the conditional expectation is
given by
.
Thus we have the conditional expectation is
given by
![\begin{displaymath}E\{\xi\vert X\} = [1-\Phi(X\beta^*)]\Phi(X\beta^*) - \Phi(X\beta^*)
[1-\Phi(X\beta^*)] = 0.
\end{displaymath}](img450.gif) |
(135) |
Thus, since the conditional expectation of y is given by the
parametric function
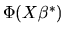 it follows from the general
results on the consistency of nonlinear least squares that the
nonlinear least squares estimator
it follows from the general
results on the consistency of nonlinear least squares that the
nonlinear least squares estimator
![\begin{displaymath}\hat\beta^n_N = \mathop{\it argmin}_{\beta \in R^k} \sum_{i=1}^N [y_i -
\Phi(X_i\beta)]^2
\end{displaymath}](img451.gif) |
(136) |
will be a consistent estimator of 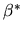 .
.
- 4.
- (20%) Derive the asymptotic distribution of the maximum
likelihood estimator by providing an analytical formula for the
asymptotic covariance matrix of the MLE estimator
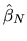
-
- Hint: This is the inverse of the information matrix
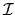 .
Derive a formula for
.
Derive a formula for 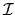 in terms of
in terms of  ,
X and
,
X and  and possibly other terms.
and possibly other terms.
-
- Answer: We know that if the model
is correctly specified and basic regularity conditions hold, that the
maximum likelihood estimator,
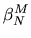 ,
is consistent and asymptotically normally
distributed with
,
is consistent and asymptotically normally
distributed with
![\begin{displaymath}\sqrt{N} [\hat \beta^m_N -
\beta^*]\phantom{,}_{\Longrightarrow \atop d} N(0,{\cal I}^{-1}),
\end{displaymath}](img455.gif) |
(137) |
where  is the Information Matrix given by
is the Information Matrix given by
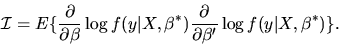 |
(138) |
In the case of the probit model we have
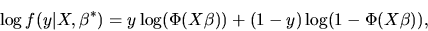 |
(139) |
and so we have
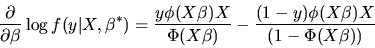 |
(140) |
where
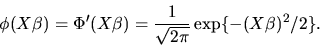 |
(141) |
Using this formula it is not hard to see that
- 5.
- (20%) Derive the asymptotic distribution of the nonlinear
least squares estimator and compare it to the maximum likelihood
estimator. Is the nonlinear least squares estimator asymptotically
inefficient?
-
- Answer: The first order condition for the
nonlinear least squares estimator
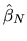 is given by:
is given by:
![\begin{displaymath}0 = {1\over N} \sum_{i=1}^N [y_i - \Phi(X_i\hat\beta_N)]
\phi(X_i\hat\beta_N) X_i.
\end{displaymath}](img463.gif) |
(143) |
Expanding this first order condition in a Taylor series about
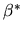 we obtain
we obtain
| 0 |
= |
![$\displaystyle {1 \over N} \sum_{i=1}^N [y_i - \Phi(X_i\beta^*)] \phi(X_i\beta^*)
X_i$](img464.gif) |
|
| |
- |
![$\displaystyle \left[ {1\over N}\sum_{i=1}^N \phi^2(X_i\tilde \beta_N)X_i X_i'
-...
...ilde \beta_N)]\phi'(X_i\tilde \beta_N)
X_i X_i'\right] (\hat\beta_N - \beta^*).$](img465.gif) |
(144) |
where
 is a vector each of who coordinates are on the
line segment joining the corresponding components of
is a vector each of who coordinates are on the
line segment joining the corresponding components of
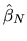 and
and
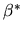 .
Solving the above equation for
.
Solving the above equation for
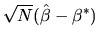 we obtain
we obtain
Applying the Central Limit Theorem to the second term in brackets in the
above equation we have
![\begin{displaymath}{1 \over \sqrt{N}} \sum_{i=1}^N \left[y_i -
\Phi(X_i\beta^*)]...
...) X_i\right]
\phantom{,}_{\Longrightarrow \atop d} N(0,\Omega),\end{displaymath}](img472.gif) |
(146) |
where 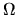 is given by
is given by
Appealing to the uniform strong law of large numbers,
we can show that the other
term in equation (145) converges to the following
limiting value with probability 1:
![\begin{displaymath}\left[ {1\over N}\sum_{i=1}^N
\phi^2(X_i\tilde \beta_N)X_i X_...
...phi'(X_i\tilde \beta_N)
X_i X_i'\right] \longrightarrow \Sigma \end{displaymath}](img476.gif) |
(148) |
where
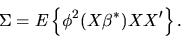 |
(149) |
It follows that the asymptotic distribution of the nonlinear least
squares estimator is given by
![\begin{displaymath}\sqrt{N}[\hat\beta_N - \beta^*] \phantom{,}_{\Longrightarrow \atop d}
N(0, \Sigma^{-1} \Omega \Sigma^{-1}).
\end{displaymath}](img478.gif) |
(150) |
Since the maximum likelihood estimator is an asymptotically
efficient estimator and the
nonlinear least squares estimator is a potentially inefficient
estimator, we have
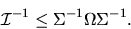 |
(151) |
To see that the inequality is strict in general, consider the
special case where there is a degenerate distribution with only
one possible X vector. Then turning the above inequality around
we want to show that
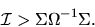 |
(152) |
However when the distribution of X is degenerate we have
![\begin{displaymath}{\cal I}= { \phi^2(X\beta^*) XX' \over
\Phi(X\beta^*)[1-\Phi(X\beta^*)]}.
\end{displaymath}](img481.gif) |
(153) |
Similarly we have
![\begin{displaymath}\Sigma \Omega^{-1} \Sigma = {\phi^2(X\beta^*) X X' \over
[1-\Phi^2(X\beta^*)] }.
\end{displaymath}](img482.gif) |
(154) |
However since
![\begin{displaymath}{1 \over \Phi(X\beta^*)[1-\Phi(X\beta^*)]} > { 1 \over
[1-\Phi^2(X\beta^*)] },
\end{displaymath}](img483.gif) |
(155) |
it follows that
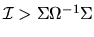 ,
so that
the nonlinear least squares estimator will generally be strictly
asymptotically inefficient in comparison to the maximum likelihood estimator.
,
so that
the nonlinear least squares estimator will generally be strictly
asymptotically inefficient in comparison to the maximum likelihood estimator.
- 6.
- (25%) Show that the nonlinear least squares estimator
of
 is subject to heteroscedasticity by deriving an
explicit formula for the conditional variance of the error term
in the nonlinear regression formulation of the estimation problem.
Can you form a more efficient
estimator by correcting for this heteroscedasticity in a two
stage feasible GLS procedure (i.e. in stage 1 computing an initial
consistent, but inefficient estimator of
is subject to heteroscedasticity by deriving an
explicit formula for the conditional variance of the error term
in the nonlinear regression formulation of the estimation problem.
Can you form a more efficient
estimator by correcting for this heteroscedasticity in a two
stage feasible GLS procedure (i.e. in stage 1 computing an initial
consistent, but inefficient estimator of  by ordinary
nonlinear least squares and in stage two using this initial consistent
estimator to correct for the heteroscedasticity and using the stage
two estimator of
by ordinary
nonlinear least squares and in stage two using this initial consistent
estimator to correct for the heteroscedasticity and using the stage
two estimator of  as the feasible GLS estimator)? If so,
is this feasible GLS procedure asymptotically efficient? If you
believe so, provide a sketch of the derviation of the asymptotic
distribution of the feasible GLS estimator. Otherwise provide a
counterexample or a sketch of an argument why you believe the
feasible GLS procedure is asymptotically
inefficient relative to the maximum likelihood estimator.
as the feasible GLS estimator)? If so,
is this feasible GLS procedure asymptotically efficient? If you
believe so, provide a sketch of the derviation of the asymptotic
distribution of the feasible GLS estimator. Otherwise provide a
counterexample or a sketch of an argument why you believe the
feasible GLS procedure is asymptotically
inefficient relative to the maximum likelihood estimator.
-
- Answer: There is heteroscedasticity in the
nonlinear regression formulation of the probit estimation problem
in (134) since we have
![\begin{displaymath}\mbox{var}(\xi\vert X) = E\{\xi^2\vert X\} = [1-\Phi(X\beta^*)]^2\Phi(X\beta^*) +
[\Phi(X\beta^*)]^2 [1-\Phi(X\beta^*)].
\end{displaymath}](img485.gif) |
(156) |
Now suppose we do an initial first step nonlinear least squares
estimation to obtain an initial  -consistent estimator
-consistent estimator
 and then use this to construct a second stage
weighted nonlinear least squares problem as follows:
and then use this to construct a second stage
weighted nonlinear least squares problem as follows:
![\begin{displaymath}\hat\beta_N^g= \mathop{\it argmin}_{\beta \in R^k} {1 \over N...
...at\beta_N) +
[\Phi(X\hat\beta_N)]^2 [1-\Phi(X\hat\beta_N)]}.
\end{displaymath}](img487.gif) |
(157) |
It turns out that this two stage, feasible GLS estimator has the
same asymptotic distribution as maximum likelihood, i.e. it is an
asymptotically efficient estimator. It is easiest to see this result
by assuming first that we know the exact form of the
heteroscedasticity, i.e. in the denominator of the second stage
we weight the observations by the inverse of the exact conditional
heteroscedasticity givein in equation (156). Then repeating
the Taylor series expansion argument that we used to derive the
asymptotic distribution of the unweighted nonlinear least
squares estimator, it is not difficult to show that
Once again, appealing to the Central Limit Theorem, we can show that
the second term in equation (158) converges in distribution
to
![\begin{displaymath}{1 \over \sqrt{N}} \sum_{i=1}^N { [y_i -
\Phi(X_i\beta^*)] \p...
...\vert X_i\}}\phantom{,}_{\Longrightarrow \atop d} N(0,\Omega),
\end{displaymath}](img490.gif) |
(159) |
where in the GLS case 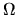 is given by
is given by
Similarly, we can show that the other term in equation (158)
converges with probability 1 to the matrix 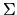 ,
,
![\begin{displaymath}\left[ {1\over N}\sum_{i=1}^N
{ \phi^2(X_i\tilde \beta_N)X_i ...
...i' \over E\{\xi_i^2\vert X_i\}}
\right] \longrightarrow \Sigma
\end{displaymath}](img495.gif) |
(161) |
where we also have
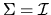 .
Thus, the GLS
estimator converges in distribution to
.
Thus, the GLS
estimator converges in distribution to
![\begin{displaymath}\sqrt{N}[\hat\beta^f_N - \beta^*]\phantom{,}_{\Longrightarrow...
...p d} N(0,\Sigma^{-1} \Omega \Sigma^{-1}) = N(0,{\cal I}^{-1}),
\end{displaymath}](img497.gif) |
(162) |
so the GLS estimator is asymptotically efficient. To show that the
feasible GLS estimator (i.e. the one using the estimated conditional
variance as weights instead of weighting by the true conditional
variance) has this same distribution is a rather tedious exercise in
the properties of uniform convergence and will be omitted.
Final Comment: I note that the GMM efficiency bound
for the conditional moment restriction
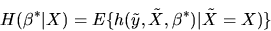 |
(163) |
coincides with
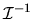 when
when
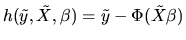 .
To see this, recall that the GMM bound
for conditional moment restrictions is given by
.
To see this, recall that the GMM bound
for conditional moment restrictions is given by
![\begin{displaymath}\left[ E\left\{ \nabla H(\beta^*\vert X) \Omega^{-1}(X) \nabla
H(\beta^*\vert X)'\right\} \right]^{-1},
\end{displaymath}](img501.gif) |
(164) |
where
 |
(165) |
and
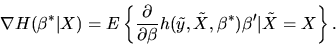 |
(166) |
In the case where
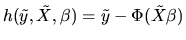 we have
we have
![\begin{displaymath}\Omega(X)= E\{\xi^2\vert X\} = [1-\Phi(X\beta^*)]^2\Phi(X\beta^*) +
[\Phi(X\beta^*)]^2 [1-\Phi(X\beta^*)],
\end{displaymath}](img504.gif) |
(167) |
that is, 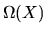 is just the conditional heteroscedasticity of the
residuals in the nonlinear regression formulation of the probit problem.
Also, we have
is just the conditional heteroscedasticity of the
residuals in the nonlinear regression formulation of the probit problem.
Also, we have
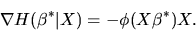 |
(168) |
Plugging these into the matrix in the inside of the expectation of the
GMM bound we have
![\begin{displaymath}\nabla H(\beta^*\vert X) \Omega^{-1}(X) \nabla
H(\beta^*\ver...
...X\beta^*) X X' \over \Phi(X \beta^*) [ 1 -
\Phi(X\beta^*)] }.
\end{displaymath}](img507.gif) |
(169) |
Taking expectations with respect to X and comparing to the
formula for the information matrix in equation (138) we see that
 |
(170) |
Since the GMM bound is the inverse of this matrix, it equals the inverse
of the information matrix,
 ,
and hence is the same
as the (asymptotic) Cramér-Rao lower bound.
,
and hence is the same
as the (asymptotic) Cramér-Rao lower bound.



Next: About this document ...
John Rust
2001-05-01
![]() are IID draws from a
are IID draws from a
![]() distribution (i.e. a normal
distribution with mean
distribution (i.e. a normal
distribution with mean ![]() and variance
and variance ![]() ). Consider the
estimator
). Consider the
estimator
![]() defined by:
defined by:

![]() ,
,
![]() is distributed as
is distributed as
![]() .
Then
.
Then
![]() is the square of
is the square of
![]() and is thus a
non-central
and is thus a
non-central ![]() random variable. Its expectation is
random variable. Its expectation is
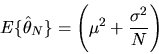
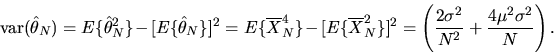
![]() is a
is a
![]() random
vector with a multivariate N(0,I) distribution, i.e.
random
vector with a multivariate N(0,I) distribution, i.e.
![]() where
0 is a
where
0 is a
![]() vector of zeros and
vector of zeros and
![]() where I is the
where I is the
![]() identity matrix. Let M be a
identity matrix. Let M be a
![]() idempotent matrix, i.e. a matrix that satisfies
idempotent matrix, i.e. a matrix that satisfies
![]() orthonormal matrix
in the singular value decompostion of the idempotent matrix M. Since
X'X=I, it follows that
orthonormal matrix
in the singular value decompostion of the idempotent matrix M. Since
X'X=I, it follows that
![]() is N(0,I). Thus,
is N(0,I). Thus,
![]() can be rewritten as
can be rewritten as
![]() .
Since D is
a diagonal matrix with J 1's K - J 0's on its main diagonal,
it follows that
.
Since D is
a diagonal matrix with J 1's K - J 0's on its main diagonal,
it follows that
![]() algebraically the sum of J IDD N(0,1) random variables and
thus has a
algebraically the sum of J IDD N(0,1) random variables and
thus has a ![]() distribution. That is, assuming without loss of
generality that the first J elements of the diagonal of D are 1's
and the remaining K-J elements are 0's we have
distribution. That is, assuming without loss of
generality that the first J elements of the diagonal of D are 1's
and the remaining K-J elements are 0's we have

![\begin{displaymath}P= \left[ \begin{array}{ccc}
1/2 & 1/3& 1/6 \\
3/4 & 0 & 1/4 \\
0 & 1 & 0 \end{array} \right] \end{displaymath}](img57.gif)
![]()
![]() .
.
![]() we have
we have
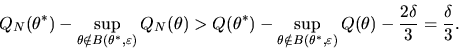
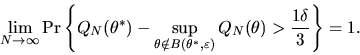
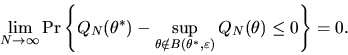
![]() is an ARMA(p,q) process, i.e.
is an ARMA(p,q) process, i.e.
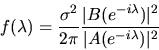
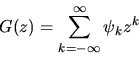
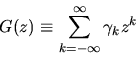
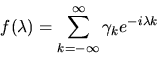
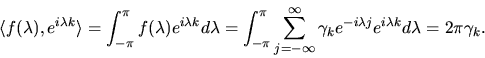
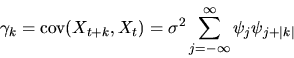
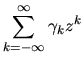

![$\displaystyle \sigma^2 \left[ \sum_{j=-\infty}^\infty \psi_j^2 +
\sum_{k=1}^\infty \sum_{j=-\infty}^\infty \psi_j
\psi_{j+k}(z^k+z^{-k}) \right]$](img141.gif)

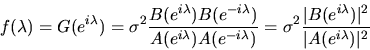
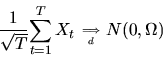
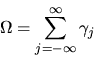
![]() ,
,
![]() .
Marketing researchers
would like to learn more about these choice probabilities,
.
Marketing researchers
would like to learn more about these choice probabilities,
![]() and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand bi chosen by shopper i,
and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand bi chosen by shopper i,
![]() .
Thus, b1=2 denotes the observation that consumer
1 chose tuna brand 2, and b4=K denotes the observation that
consumer 4 chose tuna brand K, etc.
.
Thus, b1=2 denotes the observation that consumer
1 chose tuna brand 2, and b4=K denotes the observation that
consumer 4 chose tuna brand K, etc.
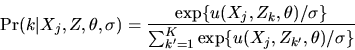
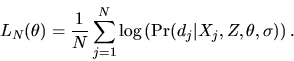
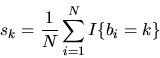
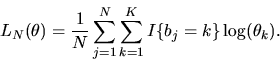
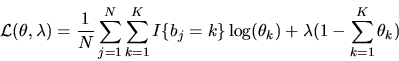
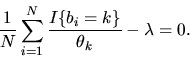
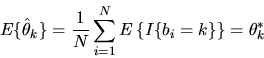
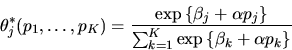
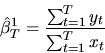

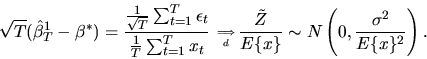
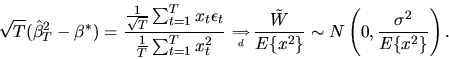
![\begin{displaymath}\sqrt{T}(\hat\beta^1_T - \beta^*) = { { 1 \over \sqrt{T}} \su...
...igma^2
E\{\vert x\vert^{\theta^*}\} \over [E\{x\}]^2} \right).
\end{displaymath}](img232.gif)
![\begin{displaymath}\sqrt{T}(\hat\beta^2_T - \beta^*) = { { 1 \over \sqrt{T}} \su...
...E\{ x^2
\vert x\vert^{\theta^*}\} \over
[E\{x^2\}]^2} \right).
\end{displaymath}](img236.gif)
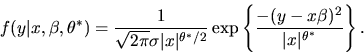
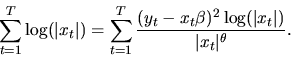
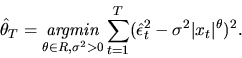
![]() are independent and identically distributed
using the moment condition
are independent and identically distributed
using the moment condition
![]() ,
where h is a
,
where h is a
![]() vector of moment conditions and
vector of moment conditions and
![]() is a
is a
![]() vector of parameters to be estimated.
Assume that the moment conditions are correctly specified, i.e. assume there
is a unique
vector of parameters to be estimated.
Assume that the moment conditions are correctly specified, i.e. assume there
is a unique ![]() such that
such that
![]() .
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically
.
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically ![]() with
J-K degrees of freedom:
with
J-K degrees of freedom:
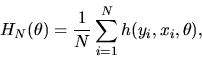
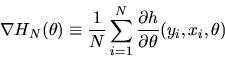
![]() given in equation (76) into the GMM first order
condition given in equation (75) and solving
for
given in equation (76) into the GMM first order
condition given in equation (75) and solving
for
![]() we obtain
we obtain
![]() ,
where
,
where
![]() is the likelihood for a single observation,
and
is the likelihood for a single observation,
and ![]() is the prior density
over
an unknown finite-dimensional parameter
is the prior density
over
an unknown finite-dimensional parameter
![]() .
.
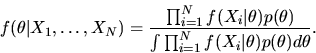
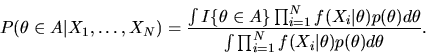
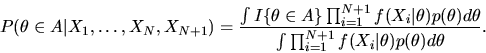
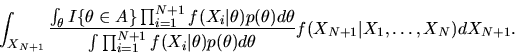
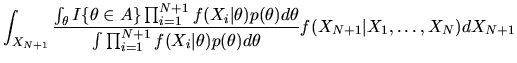
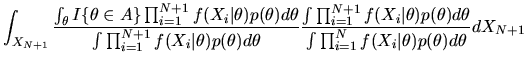
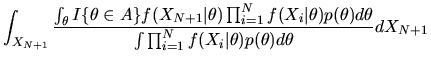
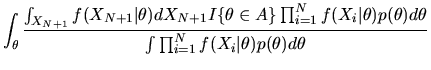
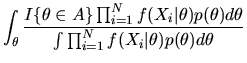
![]() and the data are generated by a multinomial
with K mutually exclusive outcomes, then the posterior distribution
after observing N IID draws from the multinomial
is also Dirichlet with parameter
and the data are generated by a multinomial
with K mutually exclusive outcomes, then the posterior distribution
after observing N IID draws from the multinomial
is also Dirichlet with parameter
![]() where
where
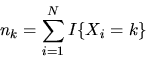
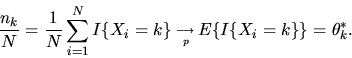
![\begin{displaymath}\lim_{N \to \infty} { 1\over N} \log\left({ p(\theta^*\vert X...
...^K
\theta^*_k \left[ \log(\theta^*_k) - \log(\theta_k)\right].
\end{displaymath}](img357.gif)
![\begin{displaymath}\sum_{k=1}^K
\theta^*_k \left[ \log(\theta^*_k) - \log(\theta_k)\right] > 0.
\end{displaymath}](img358.gif)
![]() vector
vector
![]() has a Dirichlet distribution
with
parameter
has a Dirichlet distribution
with
parameter
![]() then
then
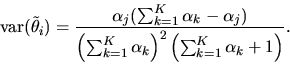
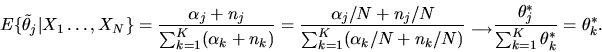

![]() is given by:
is given by:
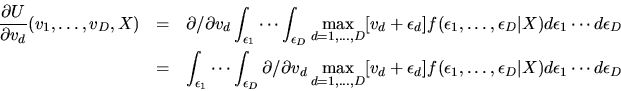
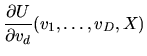
![$\displaystyle { \partial \over \partial v_d}
\int_{\epsilon_1}\cdots\int_{\epsi...
...\epsilon_d]f(\epsilon_1,\ldots,\epsilon_D\vert X)d\epsilon_1 \cdots
d\epsilon_D$](img405.gif)
![$\displaystyle \int_{\epsilon_1}\cdots\int_{\epsilon_D}
{ \partial \over \partia...
...\epsilon_d]f(\epsilon_1,\ldots,\epsilon_D\vert X)d\epsilon_1 \cdots
d\epsilon_D$](img406.gif)
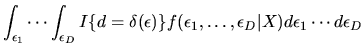

![]() are IID extreme value random variables, then
are IID extreme value random variables, then
![]() also has an extreme value distribution. Also
use the fact that the expectation of a single extreme value random
variable with location parameter
also has an extreme value distribution. Also
use the fact that the expectation of a single extreme value random
variable with location parameter ![]() and scale parameter
and scale parameter
![]() is given by:
is given by:
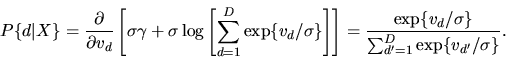
![\begin{displaymath}\mbox{Pr}\left\{ \max_{d=1,\ldots,D}[v_d + \epsilon_d] \le x\...
...\prod_{d=1}^D \mbox{Pr}\left\{ v_d + \epsilon_d \le x\right\}.
\end{displaymath}](img421.gif)
![\begin{displaymath}U(v_1,\ldots,v_D,X) \equiv E\left\{ \max_{d=1,\ldots,D}[v_d +...
...a+ \sigma\log\left[
\sum_{d=1}^D \exp\{ v_d/\sigma\} \right].
\end{displaymath}](img426.gif)
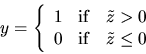
![\begin{displaymath}L(\beta) = \prod_{i=1}^N [\Phi(X_i\beta)]^{y_i}
[1-\Phi(X_i\beta)]^{(1-y_i)}. \end{displaymath}](img442.gif)
![\begin{displaymath}\hat\beta^n_N = \mathop{\it argmin}_{\beta \in R^k} \sum_{i=1}^N [y_i -
\Phi(X_i\beta)]^2
\end{displaymath}](img451.gif)
![$\displaystyle E\left\{ \left[ { 1\over \Phi(X\beta^*)} + { 1 \over
[1-\Phi(X\beta^*)]}\right] \phi^2(X\beta^*) XX' \right\}$](img461.gif)
![$\displaystyle E\left\{ \left[ { \phi^2(X\beta^*) X X'\over
\Phi(X\beta^*)[1-\Phi(X\beta^*)]}
\right] \right\}.$](img462.gif)
![\begin{displaymath}0 = {1\over N} \sum_{i=1}^N [y_i - \Phi(X_i\hat\beta_N)]
\phi(X_i\hat\beta_N) X_i.
\end{displaymath}](img463.gif)
![$\displaystyle {1 \over N} \sum_{i=1}^N [y_i - \Phi(X_i\beta^*)] \phi(X_i\beta^*)
X_i$](img464.gif)
![$\displaystyle \left[ {1\over N}\sum_{i=1}^N \phi^2(X_i\tilde \beta_N)X_i X_i'
-...
...ilde \beta_N)]\phi'(X_i\tilde \beta_N)
X_i X_i'\right] (\hat\beta_N - \beta^*).$](img465.gif)
![\begin{displaymath}{1 \over \sqrt{N}} \sum_{i=1}^N \left[y_i -
\Phi(X_i\beta^*)]...
...) X_i\right]
\phantom{,}_{\Longrightarrow \atop d} N(0,\Omega),\end{displaymath}](img472.gif)
![\begin{displaymath}\left[ {1\over N}\sum_{i=1}^N
\phi^2(X_i\tilde \beta_N)X_i X_...
...phi'(X_i\tilde \beta_N)
X_i X_i'\right] \longrightarrow \Sigma \end{displaymath}](img476.gif)
![\begin{displaymath}\hat\beta_N^g= \mathop{\it argmin}_{\beta \in R^k} {1 \over N...
...at\beta_N) +
[\Phi(X\hat\beta_N)]^2 [1-\Phi(X\hat\beta_N)]}.
\end{displaymath}](img487.gif)
![\begin{displaymath}{1 \over \sqrt{N}} \sum_{i=1}^N { [y_i -
\Phi(X_i\beta^*)] \p...
...\vert X_i\}}\phantom{,}_{\Longrightarrow \atop d} N(0,\Omega),
\end{displaymath}](img490.gif)
![$\displaystyle E\left\{ { \phi^2(X\beta^*) X X' \over
\left[ [1-\Phi(X\beta^*)]^2 \Phi(X\beta^*) + [\Phi(X\beta^*)]^2
[1-\Phi(X\beta^*)] \right]} \right\}$](img491.gif)
![$\displaystyle E\left\{ { \phi^2(X\beta^*) X X' \over \Phi(X\beta^*) [1 -
\Phi(X\beta^*)] } \right\}$](img492.gif)
![\begin{displaymath}\left[ {1\over N}\sum_{i=1}^N
{ \phi^2(X_i\tilde \beta_N)X_i ...
...i' \over E\{\xi_i^2\vert X_i\}}
\right] \longrightarrow \Sigma
\end{displaymath}](img495.gif)