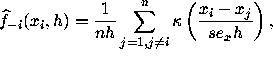 and
and 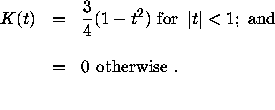 , respectively.
, respectively.
In order to be awarded DI benefits at the first stage by the DDS, an application is evaluated according to the five-stage sequential disability determination procedure illustrated in Figure 2.1 and described in section 2. For simplicity and due to data availability, we combined step 4, which evaluates the applicant's capacity to do past work, and step 5, which evaluates the applicants capacity to do any other work, into a single step 4 in our collapsed model.
Notation and specification:
Let 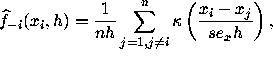 and
and ![]() be the relevant regressor vectors at
steps 1 through 4, respectively. Let
be the relevant regressor vectors at
steps 1 through 4, respectively. Let ![]() be the
probability that a person was determined as not being engaged in any
substantial or gainful activity at step 1 (that is, the person is passed on
to step 2 of the sequential process). Similarly, let
be the
probability that a person was determined as not being engaged in any
substantial or gainful activity at step 1 (that is, the person is passed on
to step 2 of the sequential process). Similarly, let ![]() be the probability that a person was determined to have severe
impairment (that is, the person is passed to step 3). At
each of the first two steps the individual can be flatly denied with
probabilities of
be the probability that a person was determined to have severe
impairment (that is, the person is passed to step 3). At
each of the first two steps the individual can be flatly denied with
probabilities of ![]() and
and 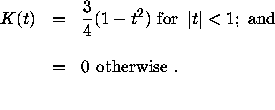 , respectively.
, respectively.
Step 3 is slightly different, in that at this step no individual is
being denied disability benefits. The DDS simply determines whether or not
the impairment(s) the individual has is (are) in the list of severe
impairments of the SSA. If the impairment(s) is (are) in the SSA listing,
then the individual is awarded disability benefits, otherwise the individual
is simply passed on to the fourth and last step, but is not denied
disability benefits. Let ![]() denote the probability
that the individual is awarded benefits at step 3.
denote the probability
that the individual is awarded benefits at step 3.
In step 4 the DDS determines whether or not an individual is
capable of performing their past job(s) or any alternative job, given the
individual's characteristics (i.e., labor market characteristics, age,
etc.). At this step the individual is either awarded or denied disability
benefits; let the probability of being awarded benefits be denoted by ![]() .
.
Define now the following dummy variables (omitting the ith subscript): ![]() if an individual is denied benefits at some step along the
five-step procedure; and
if an individual is denied benefits at some step along the
five-step procedure; and ![]() otherwise. Let
otherwise. Let ![]() if an individual
is denied benefits at step 1; and
if an individual
is denied benefits at step 1; and ![]() otherwise, and let
otherwise, and let ![]() if
an individual is denied benefits at step 2; and
if
an individual is denied benefits at step 2; and ![]() otherwise. Let
otherwise. Let ![]() if an individual is passed on (to next step) at step 3; and
if an individual is passed on (to next step) at step 3; and ![]() otherwise. Finally, let
otherwise. Finally, let ![]() if individual is denied benefits at
step 4; and
if individual is denied benefits at
step 4; and ![]() otherwise.
otherwise.
Our goal is to compute the probability of an individual being denied
benefits somewhere in the initial stage, namely, at either step 1, step 2,
or step 4, conditional on the observed data ![]() and the
model's parameter vector
and the
model's parameter vector ![]() . We denote this
probability by
. We denote this
probability by ![]() . Note that
. Note that ![]() in one of the
following three cases: (i)
in one of the
following three cases: (i) ![]() ; (ii)
; (ii) ![]() and
and ![]() or (iii)
or (iii) ![]() and
and ![]() and
and ![]() . The corresponding probabilities for
these three cases are given, respectively, by
. The corresponding probabilities for
these three cases are given, respectively, by
![]()
![]()
![]()
Therefore, we have that
![]()
where
![]()
and ![]() .
.
Assuming that the error terms of the underlying utility are distributed
according to the extreme value distribution, it follows that for each ![]() we have
we have
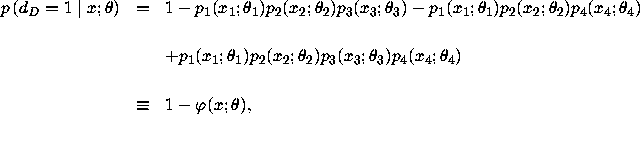 .
.
Maximum likelihood estimation:
The log likelihood function is straightforward and is given by
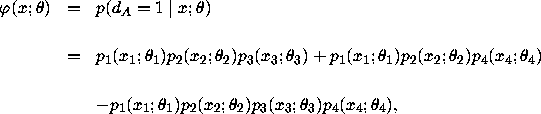
where ![]() , and
, and ![]() (i=1,...,n) are the individuals' dummy variables for being awarded
disability benefits.
The score function is given then by
(i=1,...,n) are the individuals' dummy variables for being awarded
disability benefits.
The score function is given then by
![]()
Note that 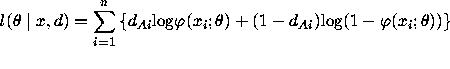 is comprised
of four separate parameter vectors, that is
is comprised
of four separate parameter vectors, that is
![]() .
.
Now, for any ![]() (j=1,2,3,4) we
have
(j=1,2,3,4) we
have 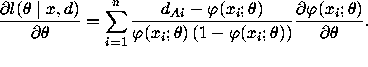 .
Hence, for
.
Hence, for ![]() we have
we have
![]()
By the standard maximum likelihood result we have that
![]() ,
where
,
where ![]() is the maximum likelihood estimator for the
population parameter
is the maximum likelihood estimator for the
population parameter ![]() and
and
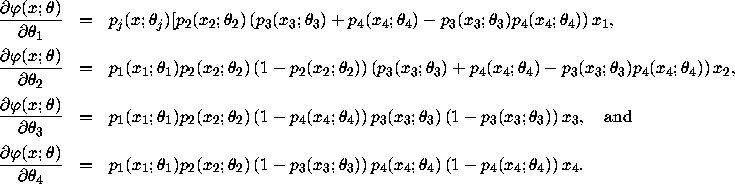
An estimate for ![]() is immediately available by the sample
analog of
is immediately available by the sample
analog of ![]() , i.e.,
, i.e.,
![]()