Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27

Proof of the Uniform Law of Large Numbers

This note presents a self-contained proof of the uniform strong law of large numbers (ULLN). The ULLN is useful in situations where we have sample moments of functions that depends on two arguments: a random element x and a deterministic parameter . Suppose we observe N IID observations from some probability distribution F(x) and we fix at some arbitrary value in the parameter space , then the ordinary strong law of large numbers (SLLN) states the following:

Strong Law of Large Numbers If , then with probability 1 we have:

The ULLN is an extension of the SLLN that provides conditions under which converges to uniformly in , i.e. conditions under which we have:

Equation (2) states that the maximum deviation between the random function and the deterministic function H converges to 0: i.e. the sequence converges uniformly in (i.e. in sup norm) to the deterministic function H. To prove (2) it is convenient to work with the normalized functions defined by

Clearly for all .

Uniform Strong Law of Large Numbers: Let be IID random elements , where X is a Borel space. Let be a measurable function of x for all , and a continuous function of for almost all . Suppose that is compact, and that converges to 0 with probability 1 for each . Then if for some function d satisfying , then we have with probability 1, i.e.

Proof: Define a function by

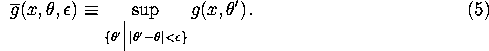
Since g is continuous in for almost all x it follows that for almost all x we have

Also, since is dominated by d(x) uniformly in , is also dominated by d(x) and we can apply the Lebesgue dominated convergence theorem to show that

Similarly we can define a function by substituting for in (5), and the result (7) will also hold for . Now consider the following inequality, which holds for all N and all sequences and all in an -ball about an arbitrary point :

Equation (8) implies the following result

Taking limits on both sides of (9) we have with probability 1:

Since and tend to 0 as by (7), given a small choose sufficiently small that both of the terms in the max expression on the right hand side of (10) are less than . Now, the collection of balls form an open cover of . By compactness, there is a finite subcover, . Since inequality (10) holds in each of these balls, we must have

Taking intersections in (11) over a sequence tending to 0, it follows that

Comment: The ULLN is actually a special case of the SLLN in Banach Spaces. That is, the functions can be regarded as random elements in the Banach space B of all continuous, bounded functions from into R. Furthermore, each of these random elements has mean zero, i.e. the expectation of the random function is the zero function , also a member of B. The SLLN in Banach spaces states the following:

SLLN for Banach Spaces Let be IID random elements in a separable Banach space satisfying (where is the 0 element of B), and . Then we have:

which is equivalent to

where is the norm of the element .

The ULLN emerges as a special case of the SLLN in Banach spaces by defining the Banach space B to be the space of all continuous functions from to R, and the norm on B is defined as the supremum norm, i.e. the maximum the absolute value of the function as ranges over . Then we can define random elements on B by and therefore the norm of these is given by

It is easy to see that the random elements satisfy the conditions of the Banach Space SLLN and therefore the sample average of these random elements converges with probability 1 to the zero element of B, , i.e. the 0 function. But the convergence in norm of the sample average of the to the element of B is equivalent to the uniform convergence of the sample average of the random functions to the zero function, which is precisely what the ULLN states. While this more abstract approach to proving the ULLN is conceptually simpler than the direct proof given above, the mathematics involved in proving the SLLN in Banach spaces are too advanced to be covered in this handout or in Econ 551.

Comment: In general, pointwise convergence of functions does not imply uniform convergence. A classic counterexample is the (deterministic) sequence of functions defined over the space by

It is clear the the sequence of functions defined in (13) converge pointwise to the 0 function, , but the sequence can't converge uniformly to since for all N. What is going wrong here is that while each is continuous, the functions are converging to a discontinous function equal to 1 at and 0 for . Another way of saying this is that the sequence is not uniformly equicontinuous.

Definition: A collection of functions mapping into R is uniformly equicontinuous if for each there exists a such that for all and for each and satisfying we have:

The key idea of equicontinuity is that inequality (14) holds simultaneously for all . There is a classical theorem of functional analysis, Ascoli's Theorem that relates uniform equicontinuity to uniform convergence:

Ascoli's Theorem: Let be a sequence of deterministic functions from to R, where is a compact subset of a Euclidean space (more generally could be a compact subset of a metric space, and in particular is allowed to be a potentially infinite-dimensional space). Then converges uniformly to a function if and only iff a) converges pointwise to H, and b) is uniformly equicontinuous. Furthermore, H is necessarily a continuous function.

Any standard textbook on functional analysis will contain a proof of Ascoli's Theorem. the proof is not difficult. We now consider a generalization of Ascoli's Theorem in the case where is a random sequence of functions. We now need to define what we mean by strong stochastic equicontinuity:

Definition: Let be a random sequence of functions from to R. We say that is weakly (uniformly) stochastically equicontinuous if

Definition: Let be a random sequence of functions from to R. We say that is strongly (uniformly) stochastically equicontinuous (SSE) if with probability 1 for all and if the sequence of random functions is weakly stochastically equicontinuous, where is defined by .

The following theorem can be viewed as the stochastic version of Ascoli's Theorem: it provides necessary and sufficient conditions for the strong uniform convergence of a sequence of random functions:

Theorem: Let be a sequence of strongly uniformly stochastically equicontinuous functions from to R, where is a compact subset of a Euclidean space (more generally could satisfy the weaker restriction of being totally bounded). Then converges uniformly to a function with probability 1 if and only iff a) converges pointwise to H with probability 1, and b) is strongly uniformly stochastically equicontinuous.

For a proof of this Theorem, see D. Andrews (1992) ``Generic Uniform Convergence'' Economic Theory 8, 241-247.

• About this document ...