Econ 551: Lecture Note 8
Increasing Efficiency of Maximum Likelihood
by Imposing Nonlinear Restrictions
1. Background: This note shows how we can increase the efficiency of maximum likelihood estimation (or any type of linear or nonlinear estimation for that matter) by imposing extra a priori information about the problem. The prior information about a problem comes in two forms:
for the observable x's.
parameters. We can write these
restrictions in the general form:
where is a 
vector and g is a 
vector: i.e. we assume we have J linear or nonlinear restrictions
on the K parameters of the model. In general J could be less than
or equal to K.
2. Asymptotic Considerations Note that imposing the
extra prior information 
is not necessary to obtain
consistency of the maximum likelihood estimator. Assuming that
the density is correctly specified, the information
inequality implies that the expected log-likelihood is maximized
at 
:
If the additional restrictions are also correctly
specified, i.e. 
, then it is easy to see that
asymptotically the constraint that is non-binding:
However in finite samples the restriction that
will generally be binding, i.e. one can generally get a higher value for
the log-likelihood of the unrestricted maximum likelihood
estimator 
defined by:
than for the restricted maximum likelihood estimator
defined by:
Lemma: Under the standard regularity conditions
for maximum likelihood (see e.g. White, 1982) and assuming the
likelihood is correctly specified, then we have:
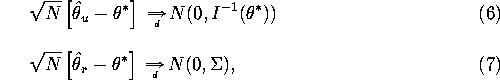
where 
is the 
information matrix given by:
is the covariance matrix given by:
and 
is the 
matrix of partial
derivatives of 
with respect to :
Proof: We have already derived the asymptotic
distribution of the unrestricted ML estimator in Econ 551, so we
restrict attention to the asymptotic distribution of the restricted
ML estimator . Note that we can convert the restricted
ML problem in equation (5) to an unrestricted optimization problem
by introducing a vector of Lagrange multipliers
and forming the Lagrangian function:
The first order or Kuhn-Tucker conditions for this constrained optimization problem are given by:
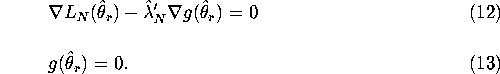
As is standard practice for determining the asymptotic distribution
of nonlinear estimators, we ``linearize'' the problem by
doing a first-order Taylor-series expansion of the Kuhn-Tucker conditions
about the limiting values of 
as 
. Since we assume the density is the true
data generating process when , then under
standard regularity conditions we can establish the uniform
consistency of 
to 
which
implies that 
with
probability 1.
If we let 
denote the Lagrange multiplier for the limiting
version of equatio (11) when , we can see from the
discussion of equations (2) and (3) that the constraint is
non-binding asymptotically, which implies that 
. So doing a
Taylor expansion of equations (12) and (13) about 
we
get:
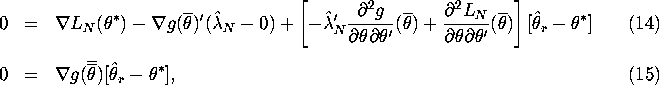
where 
and 
are points
on the line segment joining and 
.
We can write these equations in matrix form as:
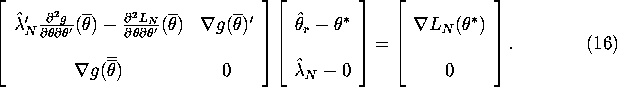
Assuming the first matrix in equation (16) is invertible, we can solve to get:
The Central Limit Theorem implies that 
. The uniform
law of large numbers implies that with probability 1 we have:
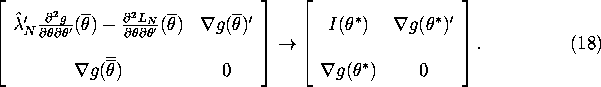
Furthermore it is straightforward to verify that the inverse of the matrix on the right hand side of (18) is given by
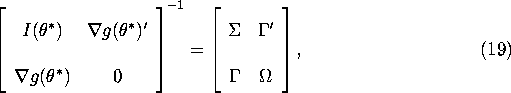
where is given in equation (9), and 
and 
are
given by:
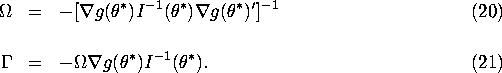
Using this formula, it is then straigthforward to verify that
as claimed in equation (7). It is obvious from equation
(9) that 
, i.e. the addition of extra a priori
information reduces the asymptotic covariance matrix of .
This is just another way of saying that
the restricted maximum likelihood estimator
is more efficient than
the unrestricted maximum likelihood esitmator .
Exercise: What is the asymptotic distribution of
?