Econ 551: Lecture Note 7
Asymptotic Efficiency of Maximum Likelihood
The Hajek Representation Theorem
1. Background: For simplicity, we will assume
a ``cross sectional framework'' where we have
IID observations 
from a ``true density'' 
, where 
is
an interior point of a compact parameter space in 
and
satisfies standard regularity conditions given,
e.g. in White (1982) ( is the unique
maximizer of 
and
is twice continuously differentiable
in 
and the expectation of the absolute value of the
hessian of is bounded by an integrable
function of x). It would be straightforward to generalize
the results presented here to time-series or heterogeneous
INID observations, but at the cost of extra assumptions
and extra notational complexity. The key maintained assumption
needed for the results below is the hypothesis of
correct specification: i.e. that is
the true data generating process for .
2. Motivation: In previous lectures I derived the
Cramer-Rao inequality and showed that the inverse of the information
matrix equals the Cramer-Rao lower bound. While this bound
holds for all N (where N is the number of observations), the
Cramer-Rao inequality can generally only be used to prove efficiency
of unbiased estimators by showing their variance equals the
Cramer-Rao lower bound. However as we noted in Econ 551, most estimators
(including most maximum likelihood estimators) are biased in finite
samples. Although the Cramer-Rao inequality holds for biased as well
as unbiased estimators, in general it is impossible to evaluate the
lower bound when estimators are biased since it involves a formula
for the bias term which is generally unknown. The Cramer-Rao lower bound
becomes more useful in large samples for consistent estimators
since consistency implies the estimators are asymptotically
unbiased. In particular we showed that maximum likelihood estimators
are consistent and asymptotically normal under weak regularity conditions.
In addition, if the parametric model is correctly specified the
asymptotic covariance matrix equals the inverse of the information
matrix. This suggests that maximum likelihood estimators are
asymptotically efficient.
3. The problem of ``superefficiency''
In Econ 551 we discussed the ``superefficiency''
counterexamples by Stein and Hodges which showed that one can
construct estimators that do better than maximum likelihood
(in the sense of having a smaller variance than the ML estimator)
if the true parameter is equal to certain isolated
points of the parameter space. A lot of effort and ingenuity has
gone into finding ways to rule out these superefficient counterexamples.
Statisticians realized that the superefficient estimators were
irregular in the sense that if the true parameter were
arbitrarily close but not equal to a point of superefficiency,
the superefficient estimator would do worse than the maximum
likelihood estimator. In other words the asymptotic distribution
of superefficient estimators can be adversely affected by
small perturbations in the true parameter . Thus,
we can rule out the superefficient counterexamples by restricting
our attention to regular estimators, i.e. those for which
the asymptotic distribution is invariant to small perturbations in
the value of the true parameter . This is formalized in the
following
Definition: An estimator 
is a regular estimator of a
parameter vector if the following conditions
hold:
, where 
is some random
vector depending on .
of
the form 
. Suppose observations
are triangular array,
i.e. IID draws from 
. Then we have
and this convergence
is uniform for 
for any constant C > 0.
Comment: It is not hard to show that all
of the ``counterexamples'' to the efficiency of maximum likelihood
estimation including the Stein estimator and the superefficient
estimator of Hodges are ``irregular'' in the sense of failing to
satisfy condition in equation (1): the asymptotic distribution of these
estimators depends on the vector , i.e. the asymptotic
distribution depends on the ``direction of approach'' of the sequence
of local alternatives 
as they converge to .
By choosing ``poor directions of approach'' we can show that there
are sequences of local alternatives for which the
superefficient estimators do worse than maximum likelihood. Of course
for our definition to make sense we need to
show that the maximum likelihood estimator is regular.
Lemma: The maximum likelihood estimator
is a regular estimator of .
Proof: (sketch) Expanding the first order condition for
about the true parameter vector and solving for 
we get:
where 
is the average of the hessian of the log-likelihood
terms and 
is a point on the line segment
between 
and .
Applying the Lindeberg-Levy Central Limit Theorem we can show that
and using the fact that the average hessian of the log-likelihood
converges uniformly to 
and converges with probability
1 to , we have that
independent of , i.e. the ML estimator is a
regular estimator of .
4. Log-Likelihood Ratios and Local Asymptotic Normality.
Hajek, LeCam and others realized that the asymptotic properties of
maximum likelihood estimators were a result of a property they
termed local asymptotic normality: i.e. the log-likelihood
ratio converges to particular a normal random variable. To state this property
formally, it it helpful to consider the following sequence of
local alternatives to formed as follows:
where 
is the information matrix.
Definition: The parametric model is said
to have the local asymptotic normality property at
iff for any 
we have:
where 
,
is the likelihood for N observations,
is the sequence of local alternatives given in equation
(5), and 
where I is the 
identity
matrix.
Lemma: If satisfies standard regularity
conditions (e.g. White 1982), then the parametric model
has the LAN property.
Proof: Expand 
in a second-order
Taylor series about we get:
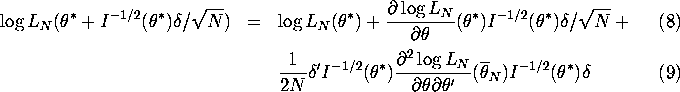
where is on the line segment between and
. Using the Central Limit Theorem it is easy to show that
the second term on the right hand side of equation (8) converges in
distribution to 
where and
I is the identity matrix. Using the uniform law of large
numbers, it is easy to show the third term on the right hand side of
equation (8) converges with probability 1 to 
.
Hajek Representation Theorem: Suppose the parametric
model has the LAN property at . Then if
is any regular estimator of we have:
where (I is the identity matrix)
and 
denotes convolution, i.e.
the random vectors 
and 
are independently
distributed.
Proof: (sketch) Since 
is assumed to be a regular estimator
of , then its asymptotic distribution does not depend on
the direction of approach of a sequence of local alternatives
where is some random vector that is
independent of the direction of approach of
to as indexed by . Let
denote the characteristic function of
, i.e.
where 
, and 
denotes the inner product of
vectors t and Y in .
from the density .
Since convergence in distribution implies
pointwise convergence of characteristic functions we have:
for each 
, where 
denotes the expectation
of with respect to the underlying random variables
which are IID draws
from . Now we can write
Notice that 
is the CF of a N(0,I) random vector.
If we can show that 
is also
a CF, then by the Inversion theorem for characteristic functions it
follows that is the CF for some
random vector 
and 
, so
the Hajek Representation Theorem (the result in equation (10)) will
follow as a special case when 
. To show that
is a CF we appeal to the
Lévy-Cramer Continuity Theorem: If a sequence of
random vectors 
with corresponding characteristic
functions 
converge pointwise to some function 
and
if is continuous at t=0, then is the characteristic
function of some random vector 
and 
.
Since is
a CF, Bochner's Theorem ( theorem providing necessary and
sufficient conditions for a function to be a CF for some random vector)
guarantees that it is continuous at t=0,
so the product
is also continuous at t=0.
So to complete the proof of the Hajek Representation Theorem we need to show
there is a sequence of characteristic functions converging pointwise
to . Let
.
Then we can write
Now here is the heuristic part of the proof (for a fully rigorous proof that justifies this step see Ibragimov, I.A. and R.Z. Khas'minskii (1981) Statistical Estimation - Asymptotic Theory Springer Verlag). By the LAN condition in equation (6) we have for large N:
where 
. So substituting equation (16) into equation (15) we get:
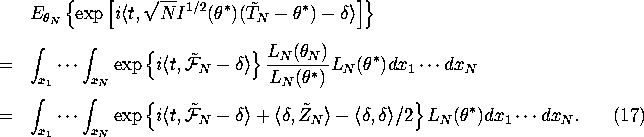
This implies that
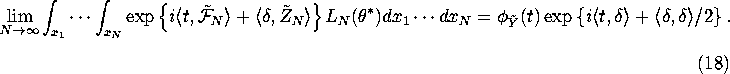
Now let 
(this can be justified by a bit of complex
analysis -- Mantel's Theorem). Then we have:
This equation states that the characteristic function of the random
vector 
converges pointwise to the function
. It follows
from the Lévy-Cramer Continuity Theorem that this function is a
characteristic function for some random vector .
In summary we have:
It follows that
so by the Lévy-Cramer continuity theorem and the inversion theorem for characteristic functions we have:
