Econ 551: Extra Credit Problem on Markov Processes and Invariant Densities
Professor John Rust, Department of Economics, Yale University
Let 
be a first order Gaussian process defined by
the linear AR(1) system:
where 
is and IID Gaussian process with
mean 0 and variance 
(i.e. 
and 
are mutually independent whenever 
and for each t we
have 
). Assume that for all t
is independent of .
a Markov process? If so, write down a formula
for its transition density 
.
is a stationary, ergodic Markov process?
? (The
recurrent class of a Markov process
is defined as the smallest closed set C such that 
, where i.o. denotes ``infinitely often''.)
is stationary and ergodic, show that
its invariant density p(y) is:
Hint: Equation (2) states that the invariant density
p(y) is normally distributed with mean 
and
variance 
. Clearly these quantities will make
sense only if 
, which should give you a pretty good
idea about how to answer question 2 above. To see why the invariant
density should be a normal distribution, use lag operators and write
equation (1) as:
where 
is the identity operator
and 
is the lag operator. If then
the operator 
is invertible and we can write
By analogy to geometric series the inverse of is given
by an infinite geometric series:
Since is an IID mean zero Gaussian process, it is
clear from equation (5) that is also Gaussian process, but
with mean and variance given by:
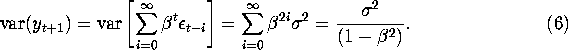
Since the time index t+1 is arbitrary, it follows from (5) and (6) that
normally distributed with mean and variance
for all t. This suggests that is in
``stochastic steady state'' and that the
distribution
for is indeed the invariant distribution of this process. However
to be rigorous, we need to verify that p(y)
defined in equation (2) satisfies the definition
of an invariant density:
This requires some tedious calculations, but you should be able
to verify that p(y) in equation (2) does indeed satisfy equation (7)
(in doing the integral in (7) you may need to make use of the
fact that a moment generating function for 
is given by 
).
Another way to guess that equation (2) gives the invariant density for this case is to assume that stationarity holds, in which case
for all s and t. Similarly
for all s and t. Using these results and the fact that
we have:
and
So stochastic stationarity implies that has mean 
and variance 
. The fact that
is Gaussian follows from the fact that is equal to a sum of
normally distributed random variables as you can see from the moving
average representation for given in equation (5).