Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27

PROBLEM SET 2

Bayesian Basics (II)

(Due: February 10, 1997)

QUESTION 1 Derive the convergence of posterior distribution when support of prior does not include true parameter 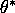. Show that

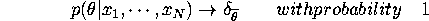
where 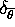is a point mass at 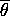and 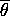is defined by:

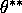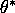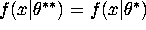QUESTION 2 Derive the convergence of posterior distribution when there exists observationally equivalent to , i.e. where for almost all x (i.e. except for x in a set of Lebesgue measure zero).

QUESTION 3 Do extra credit problem on an example of computing an invariant density for a Markov process. This is optional but recommended.

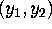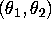QUESTION 4 This question asks you to employ the Gibbs-sampling algorithm in a simple example taken from the book Bayesian Data Analysis by Gelman et. al. Here the data consist of a single observation from a bivariate normal distribution with unknown mean and known covariance matrix 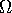given by

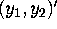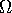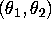With a uniform prior distribution over the posterior distribution of is bivariate normal with mean and covariance matrix . Although it is trivial to sample directly from a bivariate normal distribution of , the purpose of this question is to have you use the Gibbs sampler to draw from the posterior and compare how well the random samples from the Gibbs sampler approximate draws from the bivariate normal posterior.

1.

If 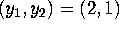and 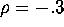, use the normal random number generator in Gauss (or some other language you are comfortable with) to draw a random sample of 500 observations from the posterior ``directly''. Report the sample mean and covariance matrix from this random sample. (Hint: you can draw from a bivariate normal with covariance matrix 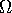by drawing a bivariate normal with covariance matrix I from Gauss's random normal generator (i.e. two independent univariate normal draws 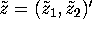) and then compute the Cholesky decomposition of 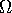, and multiply this ``square root'' matrix by 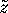to get a bivariate random draw with mean (0,0)' and covariance matrix ).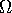

2.

Now use the Gibbs sampler to generate a random sample from the posterior. Starting from 500 points randomly, uniformly drawn over the square of width and length 1 with center (2,1) run the Gibbs sampler for 50 iterations. The Gibbs sampler is constructed by generating a draw from the normal conditional density of 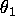given 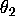given by:

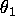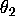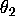Given the realized value of draw a value of from the conditional density of given 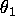given by:

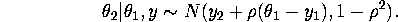
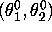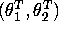Starting from 500 different randomly drawn initial values of perform T=50 loops of the above Gibbs sampling algorithm and save the 500 final draws of for each initial condition. Use these random draws to compute the sample mean and covariance matrix of the posterior. How well does it compare to the true mean and covariance matrix of the posterior? Is T=50 a sufficient number of iterations for the Gibbs sampler to converge to the invariant density?

3.

Repeat part 2, but now using T=1000 draws of the Gibbs sampler for each of the 500 randomly drawn initial conditions (save the initial conditions in part 2 in a file so you can use the same initial conditions for comparison of the the results in parts 2 and parts 3). Do you think T=1000 iterations is sufficient for the Gibbs sampler to have converged to the invariant density, i.e. the bivariate normal posterior distribution for ?

4.

Instead of using 500 different randomly chosen initial conditions, run the Gibbs sampler only once from one initial condition 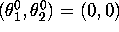for T=2500 iterations. Discard the first 2000 values of and save the last 500 values of , 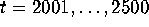. Compute the sample mean and covariance matrix of these 's. How well do they approximate the true mean and covariance matrix of the posterior density? (Here we are illustrating the principle of ergodicity i.e. if the Gibbs sampler has converged to its invariant density, then time-series averages of the random draws of the Markov process converge to their expectations, i.e. their ``long run'' expectations with regard to the invariant density. Thus, even thought the draws of are not independent for successive values of t, sample averages of these values should be close to the corresponding expectations when T is large, i.e.

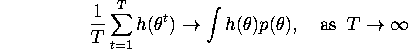
where h is some function that has finite expectation with respect to the invariant density p of the Markov process generated by the Gibbs sampling algorithm.)

• About this document ...