Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27
PROBLEM SET 4: SOLUTIONS
Classical Methods(II)
QUESTION 1 (Proof) By Chebyshev's inequality, for scalar case
or for vector case
QUESTION 2 (Proof)
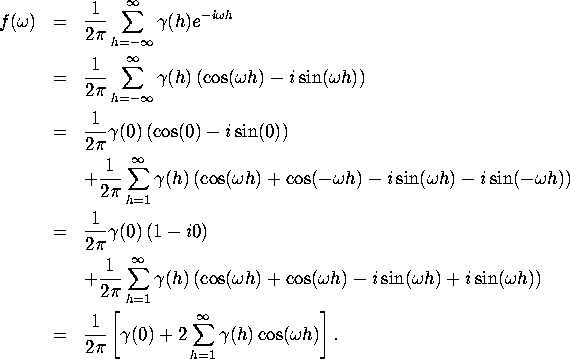
QUESTION 3 Part 1:
For the class of extremum estimator (or M-estimator) 
, following basic
consistency theorem (see Newey-McFadden(1994) for example) is available.
Theorem. If
(a) (Unique Global Maximum) limit function 
achieves a unique
global maximum at 
,
(b) (Compactness) parameter space 
is a compact set,
(c) (Continuity) limit function is continuous,
(d) (Uniform Convergence)
then 
.
Using this theorem, consistency can be proved by showing four conditions above. In our case, the criterion function is
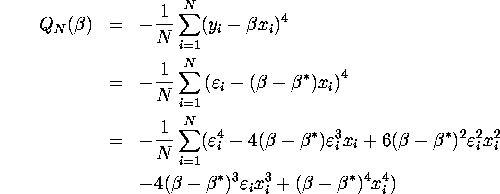
By LLN, the limit function is
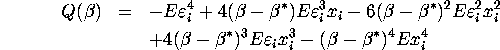
Assuming independence of 
and 
, and symmetric
distribution of the error ( 
), we have
Since coefficients on the polynomials are all negative, the limit function
is uniquely maximized at 
(uniquely global maximum).
Also the limit function is continuous (continuity). Convergence of criterion
function is uniform over compact sets of 
by virtue of the
multiplicative way in which enters (compactness and uniform
convergence). Therefore 
.
Part 2: First order condition satisfied by the estimator is
Taylor series expansion around 
yields
where 
is between and 
. Rearranging yields
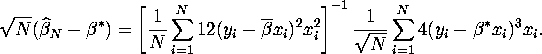
For the first (denominator) term, implies 
, and by LLN uniform in converging to , we
have
For the second (numerator) term, by CLT,
Finally by Slutsky theorem,
Part 3:
From (2) and 
and 
(this can be obtained by taking 6th derivative of normal
MGF), asymptotic variance of this M-estimator is
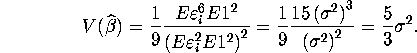
Asymptotic variance of OLS estimator is
QUESTION 4 (1) GMM estimator is in the class of M-estimators with criterion function
and limit function
where
In order to apply the basic consistency theorem for M-estimator in Question
3, we need to check each conditions by providing appropriate assumptions.
(Unique Global Maximum) By assuming 
only if 
, we have 
only if 
.
Therefore, 
for .
We now utilize following matrix ULLN.
Lemma.(Newey-McFadden p.2129) If
(a)(IID data) 
are i.i.d.,
(b)(Compactness) parameter space is a compact set,
(c)(Continuity) matrix function 
is continuous with
probability 1,
(d)(Dominating Function) there exists dominating function d(x) such that 
.
then (i) 
is continuous
and (ii)
Therefore by assuming condition (a)-(d), we have (compactness), (continuity)
(from result(i)) and (uniform convergence)(see below) for basic consistency
theorem.
(Uniform convergence)
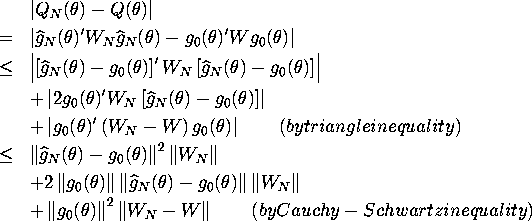
By taking supremum, result (ii) and W=p 
imply the RHS converges to zero. Therefore
Part 2: First order condition satisfied by the GMM estimator is
Taylor series expansion of 
around yields
where 
is between and 
.. Substitution to FOC implies
Rearranging yields
For the first term, implies 
, and
by LLN and continuous mapping theorem, we have
where 
.
For the second term, by CLT,
where 
.
Finally by Slutsky theorem,
Part 3: Choose 
such that 
. For example, 
where 
is the 1st stage GMM estimator with 
.
Asymptotic variance with this weight matrix reduces to 
and this achieves minimum variance bound. This can be show as
follows.
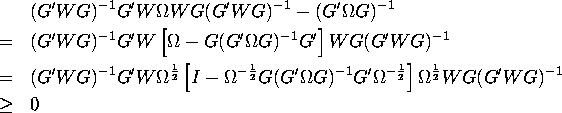
since 
is an idempotent matrix.
QUESTION 5 First order condition satisfied by the MLE is
Taylor series expansion around 
yields
where is between 
and .
Rearranging yields
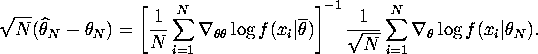
For the first term, 
implies and , and by LLN and
continuous mapping theorem, we have
For the second term, by CLT,
Finally by Slutsky theorem,
Therefore MLE is regular.
To establish this result, we need (i) 
int 
so
that 
, (ii) are independent, and (iii)
Lindeberg condition
For all 
where
in order to apply CLT for triangular array 
.