Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27
PROBLEM SET 4
Classical Methods(II)
(Due: April 13, 1997)
QUESTION 1
(Convergence) Show that if 
converges to X in quadratic mean, then also converges to X in probability.
QUESTION 2
(Spectral density) Show the following equality of spectral density:
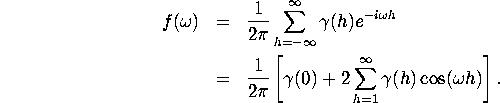
QUESTION 3
(M-estimator) Suppose following linear model:
with 
, 
is 
and 
.
M-estimator 
is defined by
where 
is a criterion function.
Let the criterion function be
(1) Show the consistency of .
(2) Derive the asymptotic distibution of .
(3) Suppose the special case where 
for all i and 
. Show that this M-estimator is less
efficient (asymptotically) than the OLS estimator.
QUESTION 4
(Generalized Methods of Moment estimator) GMM estimator 
is defined by
where
with a moment condition
where 
( 
) is the true value of 
, and 
is a 
functions of the data and parameters.
(1) Show the consistency of .
(2) Derive the asymptotic distibution of .
(3) What is optimal weight matrix 
?
Hint for (2): assume the observations 
are
IID and show that
where
QUESTION 5 Show that the maximum likelihood estimator
is regular in the sense that if
are IID draws from 
where
, then
for all 
. What conditions on and
did you need to assume to establish this result?