Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27
PROBLEM SET 2: SOLUTIONS
Bayesian Basics (II)
QUESTION 1
Define Kullback-Leibler distance by
We know equality holds only when 
.
By definition,
This implies 
.(Assume uniqueness.)
We want to show convergence of following posterior odds ratio to zero,
Since priors 
and 
do not
depend on sample size, only we need to show is the convergence of likelihood
ratio to zero,
or the convergence of the log likelihood ratio to 
,
Now,
Since
Therefore,
QUESTION 2
By the same argument,
and
Therefore,
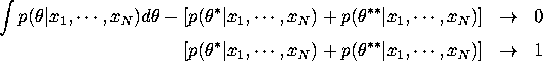
Now, observational equivalence implies
In this case, the following posterior odd ratio is identical to the ratio of priors,
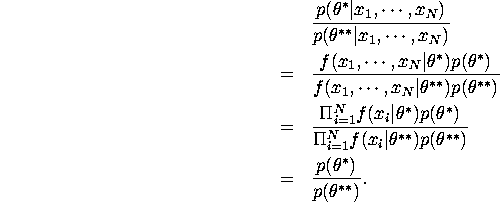
Therefore convergence of posterior distribution can be written as
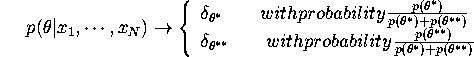
QUESTION 3
See the solution for extra credit problem.
QUESTION 4
Sample output:(See also GAUSS program)
(1) Direct method
(2) Gibbs sampler (500 initial values, 50 iterations)
(3) Gibbs sampler (500 initial values, 1000 iterations)
(4) Gibbs sampler (1 initial value, 2500 iterations)
