Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27

MIDTERM EXAM: SOLUTIONS

QUESTION 1 Seemingly unrelated regression estimator is identical to OLS estimator when regressors of all equations are identical. (Therefore you can check your SUR program by comparing SUR estimates and OLS estimates. Now, you have your own SUR program which you can use to estimate models with different regressors(!).)

We know that GLS estimator of SUR model is unbiased and efficient and can be written as

where

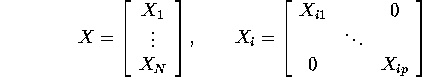
If we introduce the regressor matrices stacked by equation by equation instead of observation by observation (see solution of Q4 in Problem set 3), this estimator can be rewritten as:

where

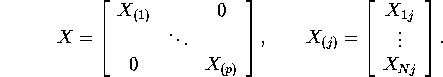
Suppose we have identical regressors, .

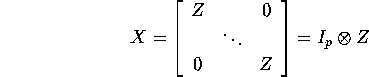
Then

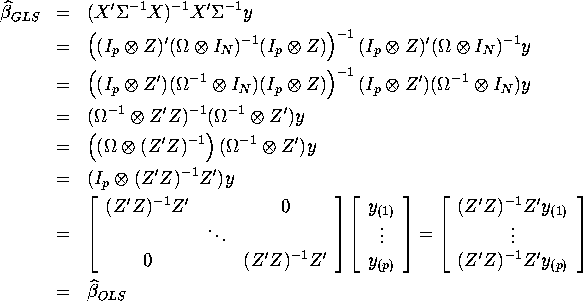
1. should be constant among equations.

2. SUR-GLS estimator or OLS estimator equation by equation from argument above.

3. Construct sample covariance matrix from OLS residuals.

4. See the calculation above.

5. I apologize for asking you to do Gibbs sampling for the full set of 63 securities: this isn't really feasible on most computers in a reasonable amount of time. With 63 securities it takes special programming to be able to run the Gibbs sampling program without using a great deal of memory space. Even when you do this the program still takes quite a bit of cpu time for the ordinary Pentium cpus in the Statlab. However if you choose a few securities from the data set, say 3 or 4 stocks, then Gibbs sampling runs reasonably quickly. Any student who just did this part using just a subset of securities in stockdat received full credit. All students who even attempted to do this part received generous partial credit, and nearly full credit if you developed a computer program to carry out the Gibbs sampling that looked correct and included it in your anwer, regardless of whether it actually worked for the problem using all 63 securities. I was more interested in getting students to write code for this problem rather than seeing actual output since the output will differ from person to person by the nature of the Gibbs sampling algorithm. I have written a program surgibbs.gpr that carries out Gibbs sampling for seemingly unrelated regression models and have the code set up to do Gibbs sampling with 3 stocks from stockdat so you can see how it runs. The program comes with 2 procedures, set_hp.g and get_dat.g which you can modify to use the software for other problems, including an artificial problem where you know the true and parameters in advance (this is useful as a check that the program is coded correctly).

QUESTION 2 Let be the number of times which outcome k occured in all sample.

With

the joint distribution of can be written as

1. Since log likelihood function is

MLE (for ) can be derived from

The solution to this system is

2.Since

Therefore is an unbiased estimator.

3.

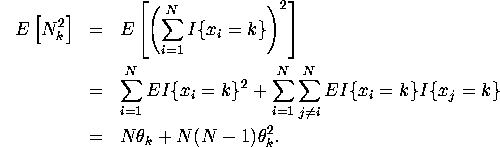
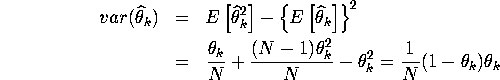
For

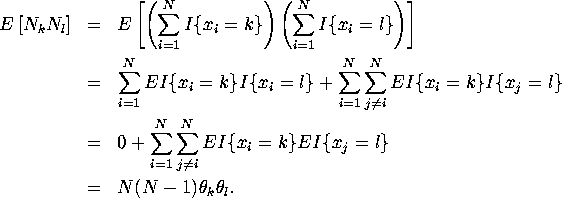
Note since at least one of and must be zero.

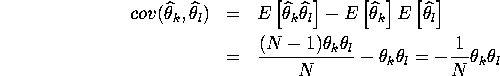
Therefore

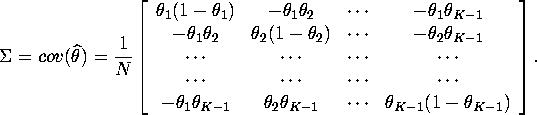
4.

For k=l

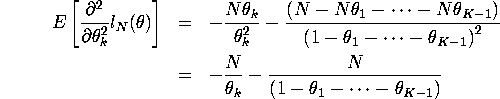
For

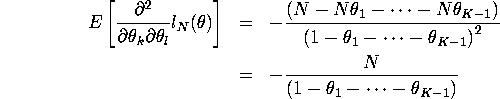
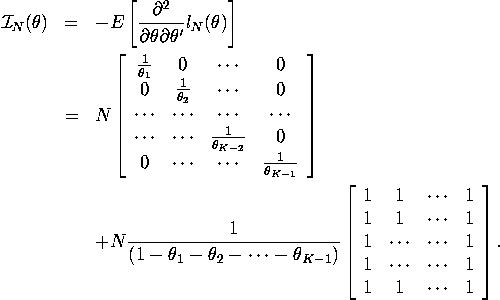
5. MLE can be proved to be efficient if it has a variance equal to Cramer-Rao lower bound. You can easily show by verifying .

6. Run the program dirichlet.gpr (which in turn calls a procedure setparm.g) available on the Econ 551 Web page. This program does the calculations required in part 6, i.e. it compares that posterior probability that (a draw from the Dirichlet posterior) is within a ball of radius .01 of the true parameter . I calculate this probability by simulation. Since this posterior probability is simulated, and since the data used to form the posterior is simulated, it makes no sense to report numbers here since they vary from run to run. The important part of this exercise is to verify that the simulated probability from the exact posterior is very close to the probability calculated from the normal approximation to the posterior.

7. First, notice that the full vector is not identified: you can add a constant to each component of and the probability in (5) will be unchanged. Therefore I impose an arbitrary normalization that and our problem reduces to the estimation of the unrestricted vector . Another arbitrary but convenient normalization is:

Under the first normalization, one can show that there is a one to one mapping between the K-1 parameters and the K-1 parameters. Thus, the by the invariance of maximum likelihood, it is easy to see that will be given by the unique solution to the K-1 system of equations

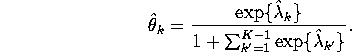
Under the second normalization we can get an explicit representation: . Since is an unbiased estimator as was verified in part 2 above, it follows from Jensen's inequality that will be a downward biased estimator of . Due to the presence of bias and the arbitrariness of the identifying normalization, it is difficult to determine whether the MLE attains the generalized Cramer-Rao lower bound in finite samples. However we know that this is a regular problem, so the MLE is asymptotically unbiased and efficient, and so does attain the Cramer-Rao lower bound asymptotically. Under the first identifying normalization, , it is easy to calculate the information matrix in this case and verify that it is the same as the inverse of the information matrix for . This should not be surprising, since the parameters are an inverse transformation of the parameters in this case. I present the derivation below. The information matrix is given by:

But we have

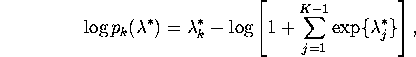
and

where is a vector of zeros with a 1 in the place. Substituting this into the equation for above we get

You can verify that this matrix is the same as the covariance matrix for given above, and as already demonstrated, this covariance matrix is the inverse of the information matrix for . So the information matrix for is the inverse of the information matrix for .

QUESTION 3

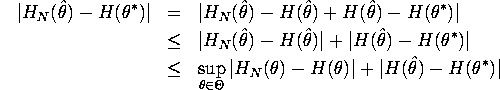
For the first term in the last inequality, with probability 1 by assumption. For the second term, H continuous and with probability 1, together implies with probability 1 by continuous mapping theorem.

Therefore with probability 1.

QUESTION 4. The Econ 551 web has Gauss programs for computing maximum likelihood estimates of the multinomial logit model plus the shell programs for running maximum likelihood. I have also posted evalbprob.g which is the procedure for computing the likelihood and derivatives for the biniomial probit model. You can run each of these programs to get the maximum likelihood estimates for the models. I have posted the estimation results for each of these programs on the Econ 551 web page.

A.

The shell program for the estimation is tnlest.gpr the procedure for calculating likelihood and derivatives of the alternative specific version of the trinomial logit model is evalmnl1.g and the output of the program is in the file data1.est all on the Econ 551 web page. The file data1.est presents estimation results for the full sample of 2,000 data points and the subsample of the first 1,500 data points. The coefficient estimates for both samples are similar, and the standard errors are higher for the the 1,500 subsample as expected. The question about the leads us into hypothesis testing. A goodness of fit test statistic would be appropriate here. But I didn't expect students to know anything about this since we haven't covered this topic at this point in Econ 551. But to anticipate, if the model is correctly specified then we should have the regression equation:

That is, is an indicator for the event that the decision taken by person i is alternative j should equal the choice probability plus an error term, . Since is the conditional expectation of , the error term must have mean zero. Therefore we can ``test'' the model both in sample and out of sample by computing the mean prediction errors, and seeing how close they are to zero:

Under standard regularity conditions, if the null hypothesis that the model is correctly specified, where is the unconditional variance of . This can be used to form a test statistic. However we need to replace the unknown true with the maximum likelihood estimate and then determine the asymptotic distribution of the corresponding statistic, doing an ``Amemiya correction'' for the fact that we are using an estimated value to construct and we need to account for this extra estimation error in the derivation of the asymptotic distribution of the test statistic. Once we do this, we can use the statistic as a ``moment condition'' and set up a hypothesis test to see how well this moment condition is satisfied. Indeed, since , we can construct an entire family of moment conditions that should be zero if the model is correctly specified. We can actually construct an entire vector of such test statistics, one for each alternative and for each instrument X that we use in forming the moment conditions. Later in Econ 551 we will show how to test all these moment conditions simultaneously using a single Chi-square goodness of fit statistic. This statistic would be the analog of the . It is important to note that we should expect the model to fit better within sample than out-of-sample since maximum likelihood is designed to choose parameters to fit a given sample of data as well as possible. In fact, with a full set of alternative specific dummies, it is easy to show that the mean prediction error for each alternative is identically zero within sample, i.e. . However is not necessarily zero if we use out of sample data, i.e. if we estimate using for and then construct using for . The program tnlest.gpr presents the mean prediction errors (by alternative) both in-sample and out-of-sample (where in sample was constructed from the first N=1500 observations and the out-of-sample was constructed from and the remaining M=500 observations in the data set. The results verify that the mean prediction errors are zero (modulo rounding error) within sample, but are non-zero out of sample. Later in the course we will post software for doing specification tests using the residuals from the estimated choice model.

B

The Econ 551 Web page has a shell program bpest.gpr and corresponding procedure evalbp.g to carry out the maximum likelihood estimation of the binary probit model. The estimation output is in the file data2.est. The true coefficient vector that was used to generate the data was (the coefficients for the first alternative were normalized to zero) and the covariance matrix of the error vector is given by

C

The Econ 551 Web page has a Gauss file surgibbs.gpr which carrys out the Gibbs sampling for the seemingly unrelated regression model. You can use this program to do Gibbs sampling on the data-augmented version of the probit model (i.e. where we treat utilities as observed) and structure the algorithm as in Rossi and McCulloch Journal of Econometrics (1994). I gave generous partial credit to any student who attempted to do this problem, and full credit to any student who developed computer code that looks correct and included it with the answer. By the way, the true coefficient vector used to generate the data was where these 6 coefficients are for the constant and slopes of the 2 X variables for alternatives 2 and 3, and the coefficients for alternative 1 were normalized to zero. The covariance matrix for the error terms in the probit model is given by:

QUESTION 5. The fact that implies that . But from earlier in the semester we know that the median is the solution to the minimization problem

Conditioning on X it follows that is the solution to the problem

so unconditionally we have:

Under assumptions of no multicollinearity between the columns of , will be the unique solution to the above minimization problem and hence is uniquely identified. Assume the observations are IID. By the uniform strong law of large numbers we have with probability 1:

where is a compact set in containing . Since is uniquely minimized at , it follows that with probability 1. For further details on the asymptotic properties of the LAD estimator (including a derivation of the asymptotic distribution of the LAD estimator), see Koenker and Bassett, ``Regression Quantiles'' in the January 1978 Econometrica.

• About this document ...