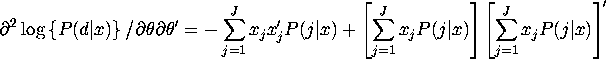Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27
HINTS TO MIDTERM EXAM
(Due: March 24, 1997)
=50000 =50000 `^Z=9
Hint for Problem 1: Use the TCP/IP ftp command to get the data set stockdat.dat and its Gauss header file stockdat.dht by anonymous ftp from gemini.econ.yale.edu as follows:
Hints on Problem 2: In part 6 of problem 2 you are
required to compute the posterior probability of being within a
ball of radius .01 about ![]() . I suggest computing this
probability by monte carlo simulations, drawing say 10,000 draws from
the Dirichlet posterior and computing the fraction that lie in the
ball of radius .01 about
. I suggest computing this
probability by monte carlo simulations, drawing say 10,000 draws from
the Dirichlet posterior and computing the fraction that lie in the
ball of radius .01 about ![]() . How do you draw from a
Dirichlet distribution? Use the following result:
. How do you draw from a
Dirichlet distribution? Use the following result:
Lemma: Let ![]() be
independent random variables, where each
be
independent random variables, where each ![]() has a gamma
distribution with parameter
has a gamma
distribution with parameter ![]() . Then the random vector
. Then the random vector
![]() has a
Dirichlet distribution with parameter
has a
Dirichlet distribution with parameter ![]() where each
where each ![]() is
defined by:
is
defined by:

Hints on Problem 4: Load the data sets data1.asc
and data2.asc by anonymous ftp following the same instructions
as above, but cd /pub/John_Rust/courses/econ551/dat and
get data1.asc and get data2.asc (there is no need to
switch to binary mode since these two data sets are in ASCII
format). You will
use data1.asc to estimate a trinomial logit model with
6 unknown alternative-specific coefficients by maximum likelihood.
To compute the maximum likelihood estimates you first need to write down the likelihood function and derivatives. Only first derivatives are required if you use BHHH but second derivatives are required if you use Newton's method. There are two ways to write down these formulae: 1) write down formulae that are specific to the case at hand, 2) write down formulae that will be useful for estimating any type of multinomial logit model with any number of alternatives.
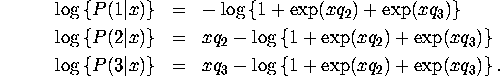
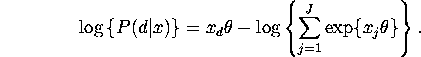

where ![]() is the original non-alternative-specific
covariate vector (dependence on observation i,
is the original non-alternative-specific
covariate vector (dependence on observation i, ![]() is supressed for clarity). It is straightforward to verify that
when the alternative-specific covariate vector
is supressed for clarity). It is straightforward to verify that
when the alternative-specific covariate vector ![]() defined above is substituted into the general formula
for the MNL log-likelihood we obtain the special
case for the trinomial logit model with alternative-specific
coefficients. We now complete the assignment by specifying the
first and second derivatives of the log-likelihood function. We
will do this for both the alternative-specific and general
forms of the MNL model.
defined above is substituted into the general formula
for the MNL log-likelihood we obtain the special
case for the trinomial logit model with alternative-specific
coefficients. We now complete the assignment by specifying the
first and second derivatives of the log-likelihood function. We
will do this for both the alternative-specific and general
forms of the MNL model.
First derivatives for
trinomial logit model with alternative-specific ![]() 's
's
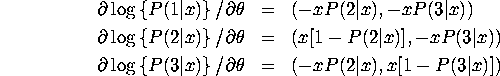
First derivatives for general MNL model
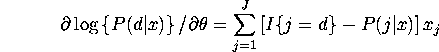
Second derivatives for
trinomial logit model with alternative-specific ![]() 's
's
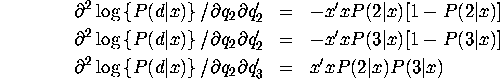
Second derivatives for general MNL model