Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27
MIDTERM EXAM
(Due: March 31, 1997)
QUESTION 1 The zero-beta version of the CAPM (capital asset pricing model) implies the following equation for security returns:
![]()
where ![]() is the realized return on security i at time t,
is the realized return on security i at time t,
![]() is the return on the market portfolio at time t,
is the return on the market portfolio at time t, ![]() is the expected return on a zero-beta portfolio, and
is the expected return on a zero-beta portfolio, and ![]() is an error term reflecting idiosyncratic risks satisfying the condition
is an error term reflecting idiosyncratic risks satisfying the condition
![]() . Assume that security returns
are serially independent, but contemporaneously correlated with
. Assume that security returns
are serially independent, but contemporaneously correlated with
![]() covariance matrix
covariance matrix ![]() , i.e.
, i.e.
![]()
where ![]() (note that serial
independence implies that
(note that serial
independence implies that ![]() if
if ![]() ). Suppose we estimate the parameters of the K regression
equations
). Suppose we estimate the parameters of the K regression
equations
![]()
so that the full vector of parameters is ![]() where
where
![]() is the
is the ![]() contemporaneous covariance matrix,
contemporaneous covariance matrix, ![]() is the
is the ![]() vector of intercepts, and
vector of intercepts, and ![]() is the
is the ![]() vector of slope coefficients.
vector of slope coefficients.
![]()
and
say binary and get stockdat.dat and get stockdat.dht
to transfer the Gauss data file stockdat.dat containing the
stock return data (a ![]() matrix for the 63 securities and
two market return indices, EQLAV and VALAV) and its
associated header file stockdat.dht (containing the names
of the securities in each column of stockdat.dat). Load the data
into gauss using the commands open f1=stockdat and
dat=readr(f1,rowsf(f1)) and put the names of the securities
(in 1 to 1 correspondence with the columns of dat) in the
vector stocknms using the Gauss command
stocknms=getname("stockdat"). (Note: if you are using Gauss
on a Unix system, you must first convert the stockdat.dat
and stockdat.dht files to Unix format. Do this by issuing the
command transdat stockdat.dat). Now
compute estimates of
matrix for the 63 securities and
two market return indices, EQLAV and VALAV) and its
associated header file stockdat.dht (containing the names
of the securities in each column of stockdat.dat). Load the data
into gauss using the commands open f1=stockdat and
dat=readr(f1,rowsf(f1)) and put the names of the securities
(in 1 to 1 correspondence with the columns of dat) in the
vector stocknms using the Gauss command
stocknms=getname("stockdat"). (Note: if you are using Gauss
on a Unix system, you must first convert the stockdat.dat
and stockdat.dht files to Unix format. Do this by issuing the
command transdat stockdat.dat). Now
compute estimates of ![]() using the methods you described in parts 2 and 3 above.
using the methods you described in parts 2 and 3 above.
QUESTION 2 Let ![]() be
IID draws from a multinomial distribution with density
be
IID draws from a multinomial distribution with density
![]()
where ![]() , the K-1-dimensional simplex (i.e. the
set of
, the K-1-dimensional simplex (i.e. the
set of ![]() satisfying
satisfying ![]() and
and ![]() ).
).
![]()
Hint 1: In parts 2 and 3 you might find the following
matrix result useful: let the ![]() matrix
matrix ![]() be
given by:
be
given by:
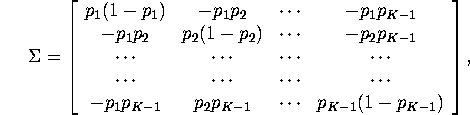
where the ![]() are positive numbers satisfying
are positive numbers satisfying
![]()
Then verify the ![]() is invertible with inverse given by:
is invertible with inverse given by:
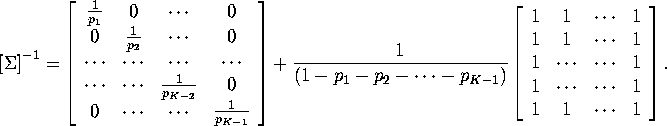
Hint 2: In part 6 you are
required to compute the posterior probability of being within a
ball of radius .01 about ![]() . I suggest computing this
probability by monte carlo simulations, drawing say 10,000 draws from
the Dirichlet posterior and computing the fraction that lie in the
ball of radius .01 about
. I suggest computing this
probability by monte carlo simulations, drawing say 10,000 draws from
the Dirichlet posterior and computing the fraction that lie in the
ball of radius .01 about ![]() . How do you draw from a
Dirichlet distribution? Use the following result:
. How do you draw from a
Dirichlet distribution? Use the following result:
Lemma: Let ![]() be
independent random variables, where each
be
independent random variables, where each ![]() has a gamma
distribution with parameter
has a gamma
distribution with parameter ![]() . Then the random vector
. Then the random vector
![]() has a
Dirichlet distribution with parameter
has a
Dirichlet distribution with parameter ![]() where each
where each ![]() is
defined by:
is
defined by:
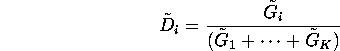
How do you draw from a Gamma distribution with parameters
![]() ? Use the fact that when
? Use the fact that when ![]() is an integer, the
Gamma distribution with parameters
is an integer, the
Gamma distribution with parameters ![]() has the representation
as the sum of
has the representation
as the sum of ![]() IID exponentials with parameter
IID exponentials with parameter
![]() , i.e.
, i.e.
![]()
where ![]() are IID exponentials
with density
are IID exponentials
with density ![]() ,
, ![]() ,
, ![]() . Note
that given the prior hyperparameters
. Note
that given the prior hyperparameters ![]() in this problem, both
the prior and posterior
in this problem, both
the prior and posterior ![]() hyperparameters will always be
integers, making it easy for you to simulate
from a Gamma an therefore from a Dirichlet.
hyperparameters will always be
integers, making it easy for you to simulate
from a Gamma an therefore from a Dirichlet.
QUESTION 3: Prove that if ![]() with probability 1, H continuous, then if
with probability 1, H continuous, then if ![]() with
probability 1, then
with
probability 1, then ![]() with probability 1.
with probability 1.
QUESTION 4.
Access simulated data from a trinomial choice model with latent
utilities ![]() given by
given by
![]()
available via anonymous ftp at gemini.econ.yale.edu. Use the cd command to go to pub/John_Rust and then cd again to the subdirectory course/econ551/dat and use the get command to retrieve the files data1.asc and data2.asc. These files contain ASCII data sets consisting of three columns, where the first column is an indicator of the chosen alternative and the remaining columns are the x covariates.
Hints: Load the data sets data1.asc
and data2.asc by anonymous ftp following the same instructions
as above, but cd /pub/John_Rust/courses/econ551/dat and
get data1.asc and get data2.asc (there is no need to
switch to binary mode since these two data sets are in ASCII
format). You will
use data1.asc to estimate a trinomial logit model with
6 unknown alternative-specific coefficients by maximum likelihood.
To compute the maximum likelihood estimates you first need to write down the likelihood function and derivatives. Only first derivatives are required if you use BHHH but second derivatives are required if you use Newton's method. There are two ways to write down these formulae: 1) write down formulae that are specific to the case at hand, 2) write down formulae that will be useful for estimating any type of multinomial logit model with any number of alternatives.
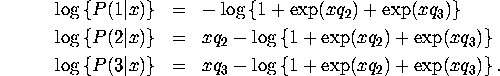
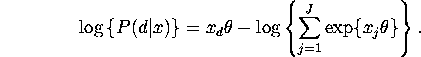

where ![]() is the original non-alternative-specific
covariate vector (dependence on observation i,
is the original non-alternative-specific
covariate vector (dependence on observation i, ![]() is supressed for clarity). It is straightforward to verify that
when the alternative-specific covariate vector
is supressed for clarity). It is straightforward to verify that
when the alternative-specific covariate vector ![]() defined above is substituted into the general formula
for the MNL log-likelihood we obtain the special
case for the trinomial logit model with alternative-specific
coefficients. We now complete the assignment by specifying the
first and second derivatives of the log-likelihood function. We
will do this for both the alternative-specific and general
forms of the MNL model.
defined above is substituted into the general formula
for the MNL log-likelihood we obtain the special
case for the trinomial logit model with alternative-specific
coefficients. We now complete the assignment by specifying the
first and second derivatives of the log-likelihood function. We
will do this for both the alternative-specific and general
forms of the MNL model.
First derivatives for
trinomial logit model with alternative-specific ![]() 's
's
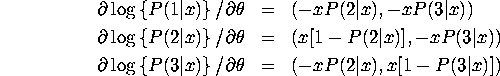
First derivatives for general MNL model
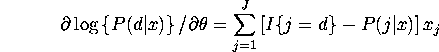
Second derivatives for
trinomial logit model with alternative-specific ![]() 's
's
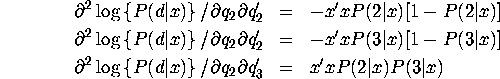
Second derivatives for general MNL model

QUESTION 5 Consider the linear regression model
![]()
where ![]() . Prove that the LAD estimator
defined by
. Prove that the LAD estimator
defined by
![]()
converges with probability 1 to ![]() .
.