


Next: About this document
Spring 1997 John Rust
Economics 551b 37 Hillhouse, Rm. 27
FINAL EXAM
April 30, 1997
INSTRUCTIONS: Answer 3 of the questions below.
Each question is worth 100 points, for a total of 300 possible points.
You have 3 hours for the exam, or 1 hour per question.
QUESTION 1 (Hypothesis testing) Consider the GMM estimator with IID data, i.e
the observations 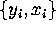 are independent and identically distributed.
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically
are independent and identically distributed.
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically  with
J-K degrees of freedom:
with
J-K degrees of freedom:
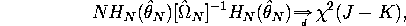
where 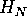 is a
is a 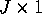 vector of moment conditions,
vector of moment conditions, 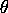 is a
is a
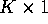 vector of parameters,
vector of parameters, 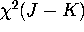 is a Chi-squared random variable with J-K degrees of freedom,
is a Chi-squared random variable with J-K degrees of freedom,
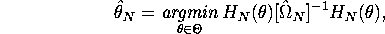

and 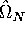 is a consistent estimator of
is a consistent estimator of  given by
given by
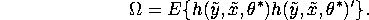
QUESTION 2 (Markov Processes)
- A.
- (10 points) Are Markov processes of any use in econometrics? Describe
some examples of how Markov processes are used in econometrics such
as providing models of serially dependent data, as a framework for establishing
convergence of estimators and
proving laws of large numbers, central limit theorems, etc.
and as computational tool for doing simulations.
- B.
- (10 points) What is a random walk? Is a random walk always a Markov process?
If not, provide a counter-example.
- C.
- (40 points) What is the ergodic or invariant distribution of
a Markov process? Do all Markov processes have invariant
distributions? If not, provide a counterexample of a Markov
process that doesn't have an invariant distribution. Can
a Markov process have more than 1 invariant distribution?
If so, give an example.
- D.
- (40 points) Consider the discrete Markov process
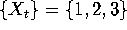 with transition
probability
with transition
probability
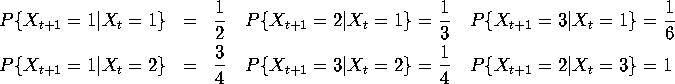
Does this process have an invariant distribution? If so,
find all of them.
QUESTION 3 (Consistency of M-estimator)
Consider an M-estimator defined by:
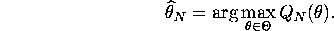
Suppose following two conditions are given
(i) (Identification) For all 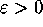
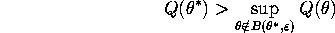
where  .
.
(ii) (Uniform Convergence)
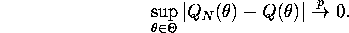
Prove consistency of the estimator by showing
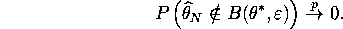
QUESTION 4 (Consistency of Bayesian posterior)
Consider a Bayesian who has observes
IID data 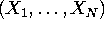 , where
, where
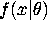 is the likelihood for a single observation,
and
is the likelihood for a single observation,
and  is the prior density
over
an unknown finite-dimensional parameter
is the prior density
over
an unknown finite-dimensional parameter  .
.
- A.
- (30 points) Let
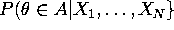 be the posterior probability
be the posterior probability
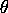 is in some set
is in some set 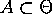 given the first
N observations. Show that this posterior probability
satisfies the Law of iterated expectations:
given the first
N observations. Show that this posterior probability
satisfies the Law of iterated expectations:

- B.
- (20 points) A martingale
is a stochastic process
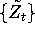 that satisfies
that satisfies
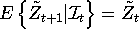 , where
, where
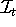 denotes the information set at time t and
includes knowledge of all past
denotes the information set at time t and
includes knowledge of all past 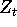 's up to time t,
's up to time t,
 . Use the
result in part A to show that the process
. Use the
result in part A to show that the process 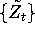 where
where
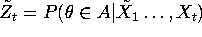 is a
martingale. (We are interested in martingales because
the Martingale Convergence Theorem can be used to show that
if
is a
martingale. (We are interested in martingales because
the Martingale Convergence Theorem can be used to show that
if 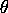 is finite-dimensional, then the posterior
distribution converges with probability 1 to a point mass on the
true value of
is finite-dimensional, then the posterior
distribution converges with probability 1 to a point mass on the
true value of 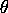 generating the observations
generating the observations 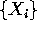 . But
you don't have to know anything about this to answer this question.)
. But
you don't have to know anything about this to answer this question.)
- C.
- (50 points) Suppose that if
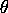 is restricted to the
K-dimensional
simplex,
is restricted to the
K-dimensional
simplex, 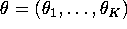 with
with 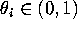 ,
,
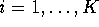 ,
, 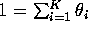 , and the distribution
of
, and the distribution
of 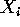 given
given 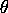 is multinomial with parameter
is multinomial with parameter 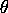 , i.e.
, i.e.
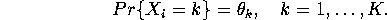
Suppose the prior distribution over 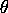 ,
,  is
Dirichlet with parameter
is
Dirichlet with parameter 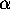 :
:
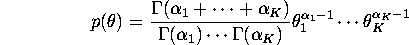
where both  and
and 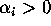 ,
, 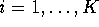 . Compute
the posterior distribution and show 1) the posterior is also
Dirichlet (i.e. the Dirichlet is a conjugate family),
and show directly that
as
. Compute
the posterior distribution and show 1) the posterior is also
Dirichlet (i.e. the Dirichlet is a conjugate family),
and show directly that
as 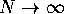 that the posterior distribution converges to
a point mass on the true parameter
that the posterior distribution converges to
a point mass on the true parameter 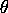 generating the data.
generating the data.
QUESTION 5 (Time series question)
Suppose 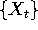 is an ARMA(p,q) process, i.e.
is an ARMA(p,q) process, i.e.

where A(L) is a 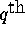 order lag-polynomial
order lag-polynomial
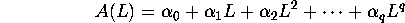
and B(L) is a 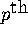 order lag-polynomial
order lag-polynomial
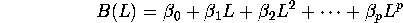
and the lag-operator 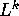 is defined by
is defined by

and 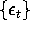 is a white-noise process,
is a white-noise process, 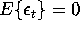 and
(cov(
and
(cov( 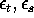 )=0 if
)=0 if 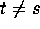 ,
, 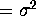 if t=s).
if t=s).
- A.
- (30 points) Write down the autocovariance and
spectral density functions for this process.
- B.
- (30 points) Show that if p = 0 an autoregression of
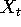 on
q lags of itself provides a consistent estimate of
on
q lags of itself provides a consistent estimate of
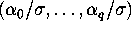 . Is the autoregression
still consistent if p > 0?
. Is the autoregression
still consistent if p > 0?
- C.
- (40 points) Assume that a central limit
theorem holds, i.e. the distribution of
normalized sums of
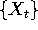 to converge in distribution to a normal random variable.
Write down an
expression for the variance of the limiting normal distribution.
to converge in distribution to a normal random variable.
Write down an
expression for the variance of the limiting normal distribution.
QUESTION 6 (Empirical question)
Assume that shoppers always choose only
a single
brand of canned tuna fish from the available selection of K
alternative brands of tuna fish each time they go shopping
at a supermarket. Assume initially that the (true) probability
that the decision-maker chooses brand k is the
same for everybody and is given by  ,
,
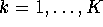 . Marketing researchers
would like to learn more about these choice probabilities,
. Marketing researchers
would like to learn more about these choice probabilities,
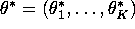 and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand
and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand 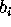 chosen by shopper i,
chosen by shopper i,
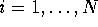 . Thus,
. Thus, 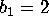 denotes the observation that consumer
1 chose tuna brand 2, and
denotes the observation that consumer
1 chose tuna brand 2, and  denotes the observation that
consumer 4 chose tuna brand K, etc.
denotes the observation that
consumer 4 chose tuna brand K, etc.
- A.
- (10 points) Without doing any estimation, are there any
general
restrictions that you can place on the
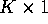 parameter
vector
parameter
vector 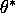 ?
?
- B.
- (10 points) Is it reasonable to
suppose that
 is the same for everyone? Describe
several factors that could lead different people to have different
probabilities of purchasing different brands of tuna. If you
were a consultant to Chicken of the Sea, what additional data
would you recommend that they collect in order to better predict
the probabilities that consumers buy various brands of tuna? Describe
how you would use this data once it was collected.
is the same for everyone? Describe
several factors that could lead different people to have different
probabilities of purchasing different brands of tuna. If you
were a consultant to Chicken of the Sea, what additional data
would you recommend that they collect in order to better predict
the probabilities that consumers buy various brands of tuna? Describe
how you would use this data once it was collected.
- C.
- (20 points) Using the observations
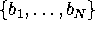 on the
observed brand choices of the sample of N shoppers, write
down an estimator for
on the
observed brand choices of the sample of N shoppers, write
down an estimator for 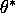 (under the assumption that
the ``true'' brand choice probabilities
(under the assumption that
the ``true'' brand choice probabilities 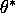 are the same
for everyone). Is your estimator unbiased?
are the same
for everyone). Is your estimator unbiased?
- D.
- (20 points) What is the maximum likelihood estimator of
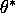 ? Is the maximum likelihood estimator unbiased?
? Is the maximum likelihood estimator unbiased?
- E.
- (40 points) Suppose Chicken of the Sea Tuna company
also collected data on the prices
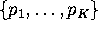 that the supermarket charged for each
of the K different brands of tuna fish. Suppose someone proposed
that the probability of buying brand j was a function of
the prices of all the various brands of tuna,
that the supermarket charged for each
of the K different brands of tuna fish. Suppose someone proposed
that the probability of buying brand j was a function of
the prices of all the various brands of tuna,
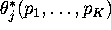 ,
given by:
,
given by:
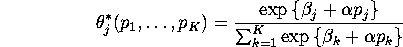
Describe in general terms
how to estimate the parameters
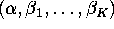 .
If
.
If 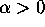 , does an increase
in
, does an increase
in 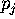 decrease or increase the probability that a shopper would buy
brand j?
decrease or increase the probability that a shopper would buy
brand j?
QUESTION 7 (Regression question)
Let 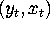 be IID observations from a regression model
be IID observations from a regression model

where  ,
, 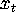 , and
, and 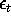 are all
scalars. Suppose that
are all
scalars. Suppose that 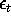 is normally
distributed with
is normally
distributed with 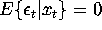 , but
, but
 .
Consider the following two estimators for
.
Consider the following two estimators for
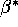 :
:


- A.
- (20 points) Are these two estimators consistent estimators of
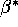 ? Which estimator is more efficient when:
1) if we know a priori that
? Which estimator is more efficient when:
1) if we know a priori that
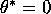 , and 2) we don't know
, and 2) we don't know 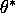 ?
Explain your reasoning for full credit.
?
Explain your reasoning for full credit.
- B.
- (20 points) Write down an asymptotically
optimal estimator for
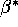 if we know the value of
if we know the value of 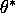 a priori.
a priori.
- C.
- (20 points) Write down an asymptotically optimal estimator for
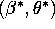 if we don't know the value of
if we don't know the value of 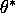 a
priori.
a
priori.
- D.
- (20 points) Describe the feasible GLS estimator for
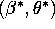 . Is the feasible GLS estimator asymptotically efficient?
. Is the feasible GLS estimator asymptotically efficient?
- E.
- (20 points) How would your answers to parts A to D change
if you didn't know the distribution of
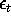 was normal?
was normal?



Next: About this document
John Rust
Mon May 5 10:40:50 CDT 1997
![]() are independent and identically distributed.
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically
are independent and identically distributed.
Show that in the overidentified case (J >K) that the
minimized value of the GMM criterion function is asymptotically ![]() with
J-K degrees of freedom:
with
J-K degrees of freedom:
![]()
![]() is a
is a ![]() vector of moment conditions,
vector of moment conditions, ![]() is a
is a
![]() vector of parameters,
vector of parameters, ![]() is a Chi-squared random variable with J-K degrees of freedom,
is a Chi-squared random variable with J-K degrees of freedom,
![]()
![]()
![]() is a consistent estimator of
is a consistent estimator of ![]() given by
given by
![]()
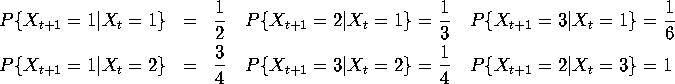
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]() , where
, where
![]() is the likelihood for a single observation,
and
is the likelihood for a single observation,
and ![]() is the prior density
over
an unknown finite-dimensional parameter
is the prior density
over
an unknown finite-dimensional parameter ![]() .
.
![]()
![]()
![]() ,
, ![]() is
Dirichlet with parameter
is
Dirichlet with parameter ![]() :
:
![]()
![]() and
and ![]() ,
, ![]() . Compute
the posterior distribution and show 1) the posterior is also
Dirichlet (i.e. the Dirichlet is a conjugate family),
and show directly that
as
. Compute
the posterior distribution and show 1) the posterior is also
Dirichlet (i.e. the Dirichlet is a conjugate family),
and show directly that
as ![]() that the posterior distribution converges to
a point mass on the true parameter
that the posterior distribution converges to
a point mass on the true parameter ![]() generating the data.
generating the data.
![]() is an ARMA(p,q) process, i.e.
is an ARMA(p,q) process, i.e.
![]()
![]() order lag-polynomial
order lag-polynomial
![]()
![]() order lag-polynomial
order lag-polynomial
![]()
![]() is defined by
is defined by
![]()
![]() is a white-noise process,
is a white-noise process, ![]() and
(cov(
and
(cov( ![]() )=0 if
)=0 if ![]() ,
, ![]() if t=s).
if t=s).
![]() ,
,
![]() . Marketing researchers
would like to learn more about these choice probabilities,
. Marketing researchers
would like to learn more about these choice probabilities,
![]() and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand
and spend a great deal
of money sampling shoppers' actual tuna fish choices in order
to try to estimate these probabilities. Suppose the Chicken of
the Sea Tuna company
undertook a survey of N shoppers and for each shopper shopping
at a particular supermarket with a fixed set of K brands of
tuna fish, recorded the brand ![]() chosen by shopper i,
chosen by shopper i,
![]() . Thus,
. Thus, ![]() denotes the observation that consumer
1 chose tuna brand 2, and
denotes the observation that consumer
1 chose tuna brand 2, and ![]() denotes the observation that
consumer 4 chose tuna brand K, etc.
denotes the observation that
consumer 4 chose tuna brand K, etc.
![]()
![]() .
If
.
If ![]() , does an increase
in
, does an increase
in ![]() decrease or increase the probability that a shopper would buy
brand j?
decrease or increase the probability that a shopper would buy
brand j?
![]() be IID observations from a regression model
be IID observations from a regression model
![]()
![]() ,
, ![]() , and
, and ![]() are all
scalars. Suppose that
are all
scalars. Suppose that ![]() is normally
distributed with
is normally
distributed with ![]() , but
, but
![]() .
Consider the following two estimators for
.
Consider the following two estimators for
![]() :
:
![]()
![]()