Prof. John Rust
Due: April 21, 1999 (Wednesday)
QUESTION 1 Derive the maximum likelihood estimator for the model
where 
are IID double exponential random
variables with mean 0 and scale parameter 
:
).
.
Hint: Show
that the MLE for 
is identical to the Least Absolute Deviations
estimator 
defined by:
QUESTION 2 Consider the random utility model:
where 
is a decision-maker's payoff or utility for selecting
alternative d from a set containing D possible alternatives (we
assume that the individual only chooses one item). The term 
is
known as the deterministic or strict utility from alternative
d and the error term 
is the random component of
utility. In empirical applications is often specified as
where 
is a vector of observed covariates and is a vector
of coefficients determining the agent's utility to be estimated. The
interpretation is that represents a vector of characteristics
of the decision-maker and alternative d that are observable
by the econometrician and 
represents characteristics
of the agent and alternative d that affect the utility of choosing
alternative d which are unobserved by the econometrician. Define
the agent's decision rule 
by:
i.e. 
is the optimal choice for an agent whose
unobserved utility components are
. Then the agent's choice
probability 
is given by:
where 
is the vector of observed characteristics of
the agent and the D alternatives and 
is the
conditional density function of the random components of utility given
the values of observed components X, and 
is the indicator function given by 
if 
and 0 otherwise.
Note that the integral above is
actually a multivariate integral over the D components of
, and simply represents the
probability that the values of the vector of unobserved utilities 
lead the agent to choose alternative d.
Definition: The Social Surplus Function
is given by:
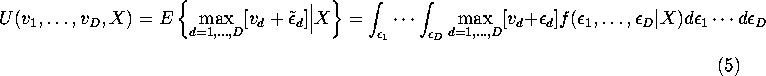
The Social Surplus function is the expected maximized utility of the
agent.
Problem: Prove the Williams-Daly-Zachary Theorem:
and discuss its relationship to Roy's Identity.
Hint: Interchange the differentiation and expectation
operations when computing 
:
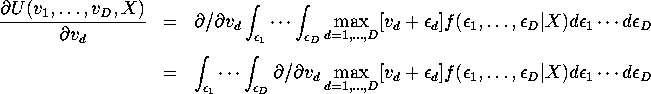
and show that
QUESTION 3 Consider the special case of
the random utility model when
has a multivariate (Type I) extreme value distribution:
Show that the conditional choice probability is given by
the multinomial logit formula:
Hint 1: Use the Williams-Daly-Zachary Theorem, showing that in the case of the extreme value distribution (8) the Social Surplus function is given by
where 
is Euler's constant.
Hint 2: To derive equation (9) show that the
extreme value family is max-stable: i.e. if 
are IID extreme value random variables, then
also has an extreme value distribution. Also
use the fact that the expectation of a single extreme value random
variable with location parameter 
and scale parameter
is given by:
and the CDF is given by
Hint 3: Let be
INID (independent, non-identically distributed) extreme value
random variables with location parameters 
and common scale parameter . Show that this family is
max-stable by proving that 
is an extreme
value random variable with scale parameter and location parameter
QUESTION 4 Extract data in data3.asc in the
directory on gemini.econ.yale.edu (either ftp to
gemini.econ.yale.edu and login as ``anonymous'' and
cd pub/John_Rust/courses/econ551/regression and
get data3.asc or click on the hyperlink in the html
version of this document). This data file
contains n=3000 IID
observations 
that I generated from the
binary probability model:
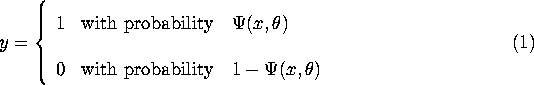
where 
is some parametric model of the conditional probability
of the binary variable y given x, i.e. 
.
Two standard models for 
are the logit and probit
models. In the logit model we have
and in the probit mode we have
where 
is the standard normal CDF, i.e.
where
More generally, could take the form
where F is an arbitrary continuous CDF.
and takes action y=1 if 
and takes action y=0 if 
.
Derive the implied choice probability 
in the case
where 
is a bivariate normal random
vector with 
, 
and 
and 
and 
.
What is the form of in the general case when
has an unrestricted bivariate normal distribution
with mean vector 
and covariance matrix 
? If the utility
function includes a constant term, i.e. 
are the 
, and parameters all separately identified
if we only have access to data on (y,x) pairs?
has a bivariate Type I extreme value distribution using the
results you have obtained from QUESTION 2 and 3.
By doing this you will have derived
the binary logit model from first principles.
compute maximum likelihood estimates of
the parameters 
of
the logit and probit specifications given in equations (2) and (3) above,
where 
is given by:
by doing
nonlinear least squares estimation of the nonlinear regression formulation
of the binary probability model
instead of doing maximum likelihood? If so, provide a proof of the consistency of the NLLS estimator. If not, provide a counterexample showing that the NLLS estimator is inconsistent.
.
consistent and asymptotically
normally distributed (assuming the model is correctly specified)?
If so, derive the asymptotic distribution of the
FGLS estimator, and if not provide a counter example showing that
the FGLS estimator is inconsistent or not asymptotically normally
distributed. If you conclude that the FGLS estimator is asymptotically
normally distributed, is it as efficient as the maximum likelihood estimator
of ? Explain your reasoning for full credit.
nonparametrically via non-parametric regression. Is there any way you
could use the nonparametric regression estimate of to help
discriminate between the logit and probit specifications?