Suggested Solution to Problem Set 3

Prof. John Rust

Econ 551b, Spring 1999

QUESTION 1 Answers given in section 9 of Rust's lecture notes, Endogenous Regressors and Instrumental Variables.

QUESTION 2 Since

log likelihood function for can be written as

MLE of , , satisfies

Therefore

QUESTION 3

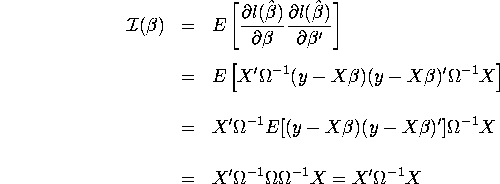
Therefore

QUESTION 4 Let be the number of times which outcome k occured in all sample.

With

the joint distribution of can be written as

1. Since log likelihood function is

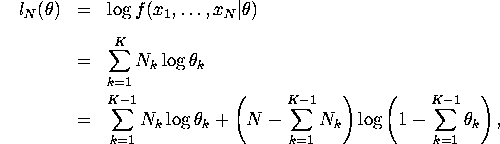
MLE (for ) can be derived from

The solution to this system is

2.Since

Therefore is an unbiased estimator.

3.

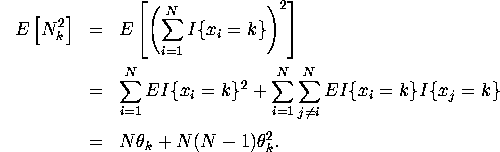
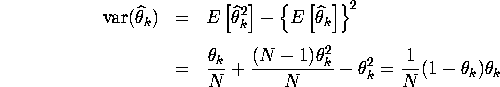
For

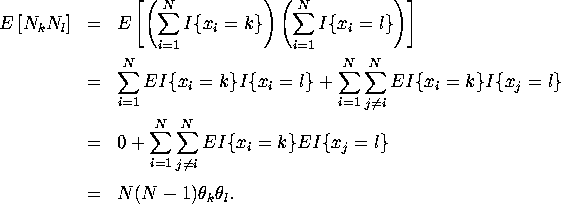
Note since at least one of and must be zero.

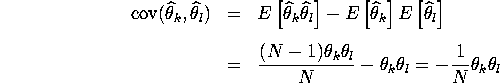
Therefore

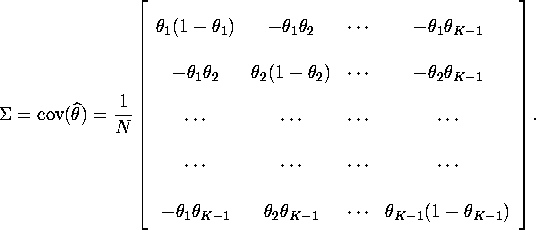
4.

For k=l

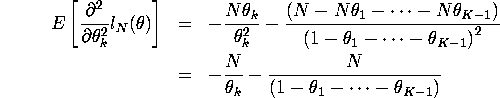
For

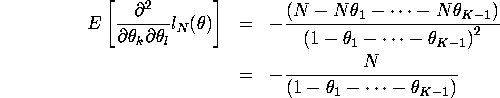
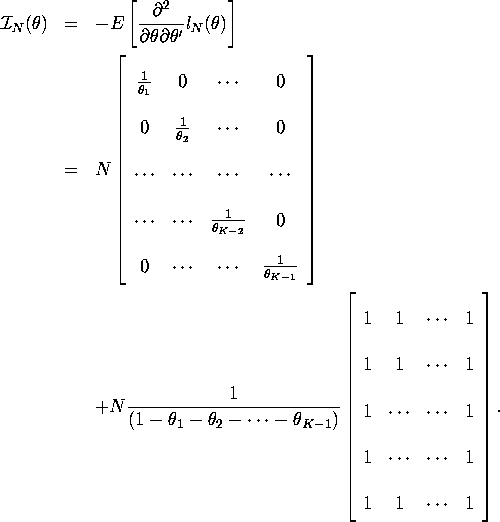
5. MLE can be proved to be efficient if it has a variance equal to Cramer-Rao lower bound. You can easily show by verifying .

• About this document ...