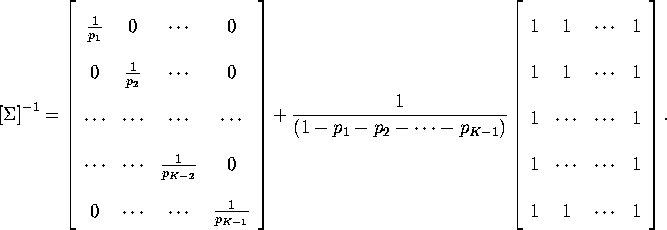Econ 551b Econometrics II
Problem Set 3

Prof. John Rust

Due: March 3, 1999

QUESTION 1 Suppose you want to estimate the regression model

where X is , using the set of instruments Z that is .

When J>=K, the generalized IV estimator is give by:

where F is a weighting matrix.

1. Find the optimal weighting matrix that minimizes variance of the estimator. The estimator using this optimal matrix is the two-stage least squares estimator.
2. Prove the consistency of the two-stage least squares estimator, and find its asymptotic distribution.
3. Show that when J=K, the two-stage least squares estimator reduces to the simple IV estimator:

   

QUESTION 2 Suppose regression model

(where y, are , X is , and is ) with normality assumption on disturbance, . Derive the maximum likelihood estimator (MLE) of when is known, and show that MLE is identical to the GLS estimator, .

QUESTION 3 Show that the Cramer-Rao lower bound, , corresponds to the GLS covariance matrix, , in Question 2.

QUESTION 4 Let be IID draws from a multinomial distribution with density

where , the K-1-dimensional simplex (i.e. the set of satisfying and ).

1.

Derive the maximum likelihood estimator for .

2.

Is the maximum likelihood estimator biased or unbiased?

3.

Derive the covariance matrix for .

4.

Derive the information matrix.

5.

Is the maximum likelihood estimator efficient? If not, find a more efficient estimator for .

Hint: In parts 2 and 3 you might find the following matrix result useful: let the matrix be given by:

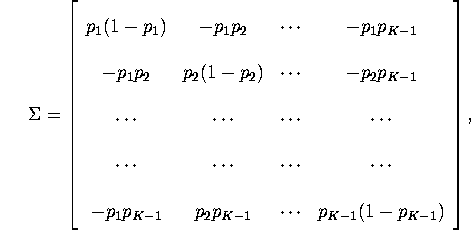
where the are positive numbers satisfying

Then verify that is invertible with inverse given by:

• About this document ...