Prof. John Rust, Hiu Man Chan
Spring, 1999
Question 1
By Jordan decomposition:
where D is a diagonal matrix with eigenvalues on the diagonal:
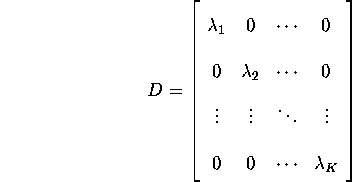
and X is orthogonal. Since 
is positive definite,
all the eigenvalues are positive. Therefore we can define
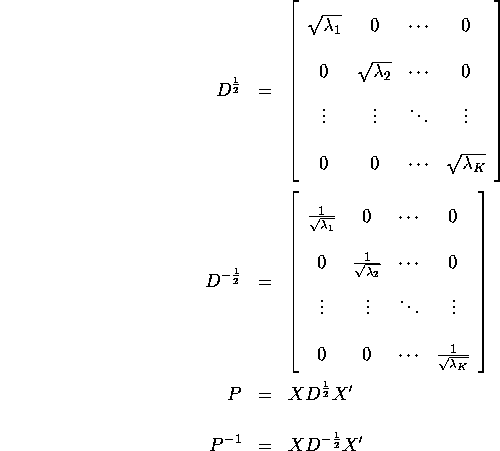
We can then have the following decomposition:
Now we know 
vector 
, and each element of Z , 
for all 
.
Therefore,
Question 2
Given vectors 
, 
, 
,..., we can obtain orthogonal vectors
, 
, 
,... through the following method:
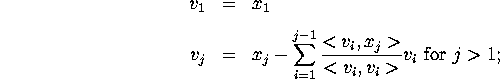
Given 1, x, 
, 
,..., note that
Plugging into the formula, we can obtain the first four orthogonal vectors (the Legendre Polynomials):
Each of these is then normalized to give the final result:
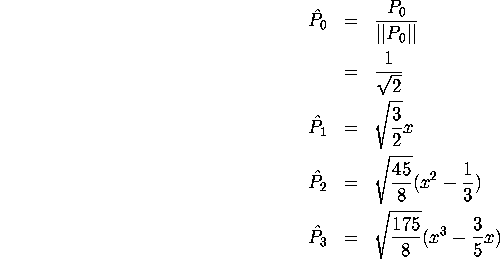
Question 3
OLS estimates are obtained from the normal equations:
Solving the above system gives:
where
Estimates from stepwise regression are given by:
Therefore
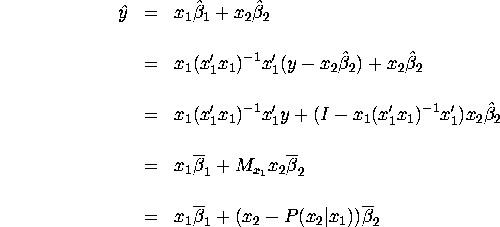
Stepwise regression can be useful when we care only about the predicted value of the dependent variable, but not the coefficients of the independent variables. Since the predicted value can be obtained by a series of estimations with a smaller number of independent variables, it is computationally less demanding.
Question 4
The solution can be found in Section 1.6 of Brockwell and Davis.