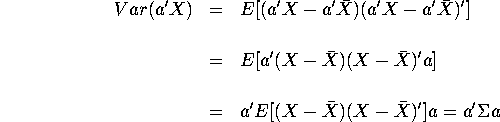

The symmetric matrix is not positive semi-definite. E.g., by putting in x=1 and y=0, the expression gives negative values.
Prof. John Rust, Hiu Man Chan
Econ 551b, Spring 1999
Question 1
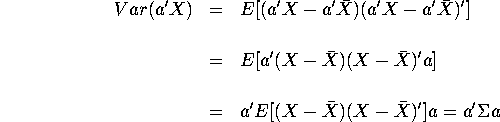

The symmetric matrix is not positive semi-definite. E.g., by putting in x=1 and y=0, the expression gives negative values.
Question 2
A sample GAUSS program is attached for your reference.
Graphs of empirical distributions of OLS estimates are
also attached.
Summary Statistics of OLS estimates from the Montel Carlo experiment are:
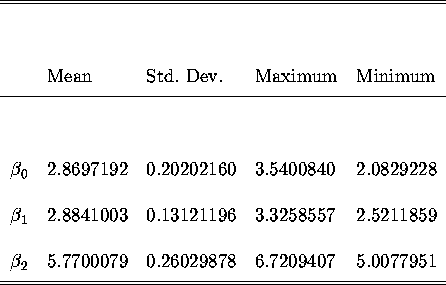
Comparing with the true parameter values, it's clear
that we are getting biased and inconsistent estimates.
Question 3
Please refer to the sample GAUSS program for this question.
The assumptions made include ![]() and
and ![]() , and that
, and that ![]() are i.i.d.
Under these assumptions, OLS estimates will
have a lot of nice properties, including BLUE, consistency and
asymptotic normality. This is also a simple start to make
estimation easier.
But you should bear in mind when you conduct serious research in
the future that many of these assumptions
are far too restrictive.
are i.i.d.
Under these assumptions, OLS estimates will
have a lot of nice properties, including BLUE, consistency and
asymptotic normality. This is also a simple start to make
estimation easier.
But you should bear in mind when you conduct serious research in
the future that many of these assumptions
are far too restrictive.
In my estimation, the dependent variable, a measure of earning power, is given by the hourly wage of the individual (earnings divided by total number of hours worked). Explanatory variables include:
For each variable, I have screened out invalid response. Also, I have
screened out respondents who work less than 1600 hours, as I believe
these are part-time workers and the wage determination of full and part
time may be very different. As one of you observed, there are some outliers
who earn a whole lot than others. I eliminate the observation of the
individual with the highest hourly wage (that person earned an hourly
wage of $3400, while the mean hourly wage is just $20). Such outliers
can imply coding error. Even if it is coded correctly, the error is
too noisy to be added in.
The results of the OLS regression are as follows:
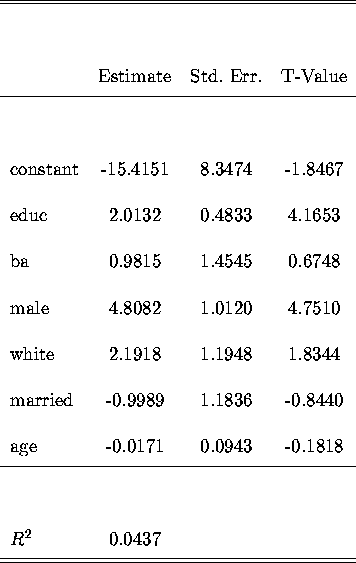
The education variables, educ and ba, are significant and of the sign we
expect. More education brings higher earning power. The other
education variable, voctrn, is not included because of missing values.
Voctrn it is not a variable as good as the other two
due to the fact that vocational training are likely to be
received for people in occupations with low income, so the variable can
be endogenous, and the positive
effect of traning on income is blurred. The result also shows that male
and white receive significantly higher earnings than female and non-white.
Married people have lower earnings, but not very significant. Finally, age is
insignificantly negative. Probably age is not a good variable to
include. On the one hand, older people may have more work experience,
hence higher earnings. But older people's productivity may be
declining, bringing lower earnings. The overall effect is really
ambiguous.
The regression model explains only ![]() of the variation in earning
power. This can signal a lot of missing variables, like occupation,
skills, and quality of education. Omitted variables can lead to biased
and inconsistent
estimates. The bad fit can also signal the fact that the model is not
linear. Again, this can lead to biasedness and inconsistency. For more
careful research, we should proceed to improve our linear regression
model, and to collect more relevant explanatory variables.
of the variation in earning
power. This can signal a lot of missing variables, like occupation,
skills, and quality of education. Omitted variables can lead to biased
and inconsistent
estimates. The bad fit can also signal the fact that the model is not
linear. Again, this can lead to biasedness and inconsistency. For more
careful research, we should proceed to improve our linear regression
model, and to collect more relevant explanatory variables.