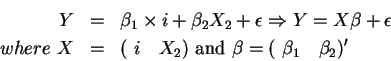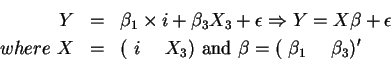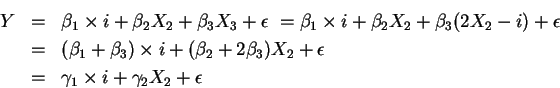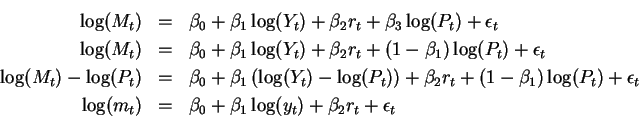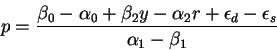![\begin{displaymath}X'X = \left[
\begin{array}{cc}
24 & 0 \\
0 & 2
\end{array}\...
...uad
X'y = \left[
\begin{array}{c}
1 \\
3
\end{array}\right].
\end{displaymath}](img2.gif)
From the result in a), we know the diagonal matrix X'X has the simple inverse matrix given by
![\begin{displaymath}\left[
\begin{array}{cc}
1/24 & 0 \\
0 & 1/2
\end{array}\right].
\end{displaymath}](img3.gif)
Therefore, we have
![\begin{displaymath}\widehat{\beta }=(X^{\prime }X)^{-1}X^{\prime }y=\left[
\beg...
...ht] =\left[
\begin{array}{c}
1/24 \\
3/2
\end{array}\right].
\end{displaymath}](img4.gif)
![\begin{displaymath}\widehat{\beta }=(X^{\prime }X)^{-1}X^{\prime }y=\left[
\beg...
..._{1}^{^{\prime }}y \\
X_{2}^{^{\prime }}y
\end{array}\right].
\end{displaymath}](img12.gif)
But using our results in a), we get
![\begin{displaymath}\widehat{\beta }=\left[
\begin{array}{cc}
(X_{1}^{^{\prime }...
...y \\
(X_{1}^{^{\prime }}X_{1})^{-1}X_{1}y
\end{array}\right].
\end{displaymath}](img13.gif)
Therefore, the blockwise diagonality condition allows us to treat the two sets of regressors separately. As a special case, when we have K regressors all orthogonal to each other as in the pard f) below, we can estimate each of the K regression coefficients by
or in a matrix form,
![\begin{displaymath}y=\left[
\begin{array}{cccc}
D_{1} & D_{2} & ... & D_{K}
\en...
...\\
\beta _{1} \\
\ldots \\
\beta_{1}
\end{array}\right] +e
\end{displaymath}](img16.gif)
The mutual exclusiveness of the dummy variables implies
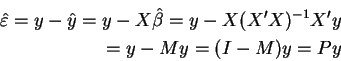
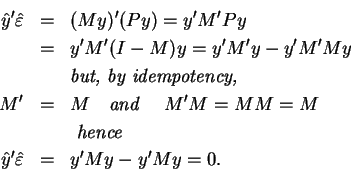
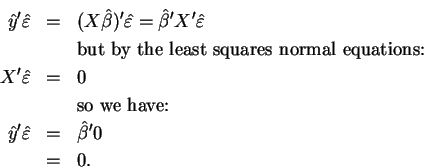
![\begin{displaymath}{y \atop 3 \times 1}=\left[
\begin{array}{l}
3 \\
2 \\
3
\...
...n _{1} \\
\epsilon _{2} \\
\epsilon _{3}
\end{array}\right].
\end{displaymath}](img66.gif)
![\begin{displaymath}X^{\prime }X=\left[
\begin{array}{ll}
4 & 0 \\
0 & 4
\end{array}\right].
\end{displaymath}](img67.gif)
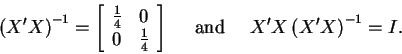
![\begin{displaymath}\widehat{\beta }=\left( X^{\prime }X\right) ^{-1}X^{\prime }y...
...\left[
\begin{array}{c}
\frac{3}{2} \\
1
\end{array}\right]
\end{displaymath}](img70.gif)
![\begin{displaymath}\widehat{y}=X\widehat{\beta }=\left[
\begin{array}{ll}
2 & 0...
...t] =\left[
\begin{array}{c}
3 \\
2 \\
0
\end{array}\right]
\end{displaymath}](img71.gif)
![\begin{displaymath}\widehat{\epsilon }=y-X\widehat{\beta }=\left[
\begin{array}{c}
0 \\
0 \\
3
\end{array}\right]
\end{displaymath}](img72.gif)
![\begin{displaymath}i^{\prime }\widehat{\epsilon }=\left[
\begin{array}{lll}
1 &...
...[
\begin{array}{c}
0 \\
0 \\
3
\end{array}\right] =3\neq 0
\end{displaymath}](img73.gif)
![\begin{displaymath}Z_{1}^{\prime }\widehat{\epsilon }=\left[
\begin{array}{lll}...
... \left[
\begin{array}{c}
0 \\
0 \\
3
\end{array}\right] =0
\end{displaymath}](img76.gif)
![\begin{eqnarray*}P &=&X(X^{\prime }X)^{-1}X^{\prime } \\
&=&\left[
\begin{arra...
...y}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right]
\end{eqnarray*}](img79.gif)
![\begin{displaymath}Py=\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 &...
...begin{array}{c}
3 \\
2 \\
0
\end{array}\right] =\widehat{y}
\end{displaymath}](img80.gif)
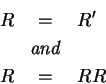
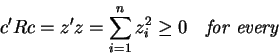
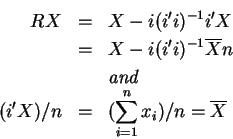
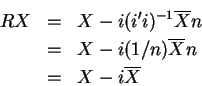
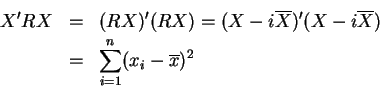
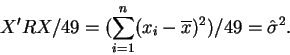
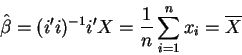
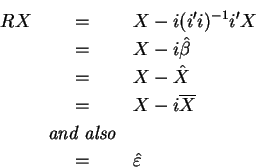
![\begin{eqnarray*}Y &=&\beta _{1}\times\vec{i}+\beta _{2}X_{2}+\beta _{3}X_{3}+\e...
...
9 \\
11 \\
13 \\
15 \\
17 \\
19 \\
21
\end{array}\right]
\end{eqnarray*}](img109.gif)