


Next: About this document
Economics 551 Professor Rust
Spring 1999
Midterm Exam
(Due at start of class, February 24, 1999)
Part I: Regression Questions (computers not required for
this part)
Do Question 1 and 2 out of 3 of the remaining Part I
questions below.
Question 1 (200 points).
- a.
- Compute the OLS estimates
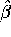 for the following 2-variable linear regression problem:
for the following 2-variable linear regression problem:
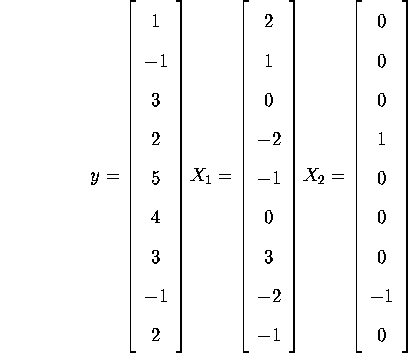
- b.
- Unfortunately, there was one student who didn't know how to
invert a
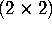 matrix. Thinking that it would be unnecessary to estimate
matrix. Thinking that it would be unnecessary to estimate 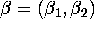 as a whole, he proposed the following
estimation formulas:
as a whole, he proposed the following
estimation formulas:
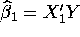 /
/ 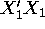 , and
, and
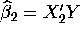 /
/ 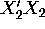 .
.
Calculate these ``naive'' estimators of
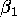 and
and 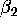 and compare them with those obtained in b.
and compare them with those obtained in b.
- c.
- What do you think about his approach? Will it work generally? Will the naive estimators be unbiased and consistent? If not,
specify the conditions needed to justify his approach. What's the intuition
behind those conditions?
- d.
- How can you generalize your argument in d to the case of a k-variable
linear regression model?
- e.
- Show that if a regression contains a set of K mutually
exclusive dummy variables
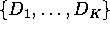 where the
variables are mutually exclusive in the sense that
if
where the
variables are mutually exclusive in the sense that
if 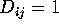 (observation i is 1 for the
(observation i is 1 for the 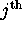 dummy
variable), then
dummy
variable), then 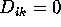 for all
for all 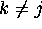 (i.e. all of the
other dummy variables dummy take the value 0 for observation i),
then the K OLS regression estimates
(i.e. all of the
other dummy variables dummy take the value 0 for observation i),
then the K OLS regression estimates 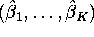 in the regression
in the regression
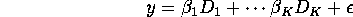
are given by
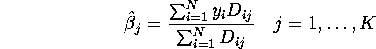
Show that 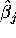 is just the mean of y over the subpopulation
of individuals i with
is just the mean of y over the subpopulation
of individuals i with 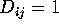 .
.
Question 2. (100 points) Consider the general multivariate regression model

- a.
- Suppose you estimate the OLS estimate of
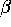 ,
, 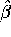 , and then compute
, and then compute 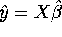 ,
the
,
the 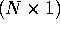 vector of predicted values of y,
and
vector of predicted values of y,
and 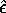 , the
, the 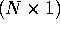 vector of error terms,
vector of error terms, 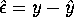 .
.
- 1.
- What is the value of the inner product of
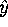 and
and 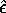 ?
?
- 2.
- Justify your answer in part a-1 above. You can either use a geometric argument or an
algebraic derivation. Can you give an intuitive explanation for
your result?
- 3.
- What are the implications of your answer for regression analysis ?
- b.
- Consider now the quantity
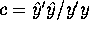 .
.
- 1.
- Show that c has to be between zero and one by using your
answer to part a above. (Hint: use the pythagorean
theorem.)
- 2.
- Does c provide any sort of measure of ``goodness of
fit'' of the regression model? Explain your answer for full credit.
What is the interpretation of the case where c=0? What is the
interpretation of the case where c=1?
Question 3 (100 points).
This question considers a regression through the origin and the
connection with the geometric notion of
projection in three dimensional space. You should be able to answer
this question using simple matrix algebra, without the use of a computer.
Consider the following model:
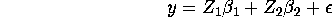
where

- a.
- Write the model in the form
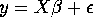 using matrices. Specify these
matrices and their dimensions.
using matrices. Specify these
matrices and their dimensions.
- b.
- Calculate (X'X) and its inverse. Verify that
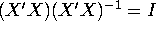 where I is the
where I is the 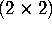 identity matrix.
identity matrix.
- c.
- Derive the least squares estimates
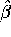 and the predicted value
and the predicted value 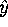 .
.
- d.
- In a three dimensional diagram, display the following:
- 1.
- the subspace S spanned by the columns of X (shade region).
- 2.
- the vectors y,
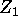 and
and 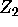 and
and 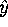 .
.
- 3.
- the orthogonal projection of y onto the subspace S
sketched in part d-1 above.
- e.
- Derive the vector of residuals
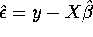 and calculate:
and calculate:
- 1.
-
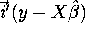 where
where 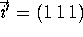 . Does
. Does
 lie in the subspace spanned by the
columns of X? Does your result for the value of
lie in the subspace spanned by the
columns of X? Does your result for the value of
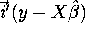 shed any light on this?
shed any light on this?
- 2.
-
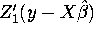 . Is this equal to zero? Explain your
answer in either case.
. Is this equal to zero? Explain your
answer in either case.
- f.
- The orthogonal projection of y into the subspace S spanned by the columns of the matrix X is given
by
 . Calculate Py and verify that
. Calculate Py and verify that 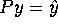 .
.
- g.
- A symmetric square matrix A is idempotent if A'A = A. Show that
P given above is
idempotent. Calculate the rank of P. Is P an invertible matrix?
Question 4. (100 points) The following questions concern
OLS estimation of the general linear model

where y is 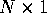 , X is
, X is 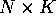 and
and  is
an
is
an 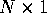 vector of error terms.
vector of error terms.
- a.
- What happens when we try to
do OLS when the
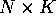 regressor matrix X has rank less than
K? Is the X'X matrix invertible in this case?
If not, does the OLS estimate
regressor matrix X has rank less than
K? Is the X'X matrix invertible in this case?
If not, does the OLS estimate 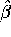 exist?
exist?
- b.
- Does the problem of multicollinearity
have anything to do with the rank of X?
- c.
- Show that when X'X is not invertible there are generally
infinitely many solutions to the normal equations for the
OLS estimator.
- d.
- Does the best fitting predicted y,
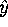 , exist when
X'X is not invertible? If yes, can you provide a formula for
, exist when
X'X is not invertible? If yes, can you provide a formula for
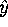 or a procedure for computing it?
or a procedure for computing it?
- e.
- Define what is meant by the generalized inverse,
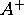 of a square matrix A.
Is the
of a square matrix A.
Is the 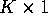 vector
vector 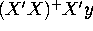 a solution to
the normal equations if X'X is not invertible?
a solution to
the normal equations if X'X is not invertible?
- f.
- Describe the process of stepwise regression and
discuss whether this procedure will allow us to compute the
predicted values of the dependent variable,
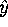 . If X'X
is invertible, will the coefficients produced by stepwise
regression coincide with the coefficients from the standard
OLS formula
. If X'X
is invertible, will the coefficients produced by stepwise
regression coincide with the coefficients from the standard
OLS formula 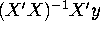 ?
?
Applied Regression/Instrumental Variable Questions
(computers required for this part)
Do Question 0 and Question 1 or 2 and Question 3 or 4
Question 0. (200 points) Given an 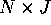 matrix
of instruments and an
matrix
of instruments and an 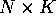 matrix of endogenous
regressors we form the instrumental variables estimator.
matrix of endogenous
regressors we form the instrumental variables estimator.
- a.
- What is the equation for
the instrumental variables estimator? Consider
separately the three cases, J=K, J > K and J < K.
- b.
- In the overidentified case, J > K, we have more instruments
than endogenous regressors. Suppose we form a
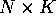 matrix
of instruments
matrix
of instruments 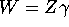 for some
for some 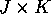 matrix
matrix 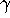 .
Derive the formula for the class of IV estimators and show
how it depends on the choice of
.
Derive the formula for the class of IV estimators and show
how it depends on the choice of 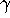 . Is there an ``optimal''
choice for
. Is there an ``optimal''
choice for 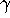 ? If so, describe what the optimal
? If so, describe what the optimal
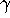 is and in what sense
this choice is optimal.
is and in what sense
this choice is optimal.
- c.
- Sketch the argument for showing the consistency and asymptotic
normality of the IV estimator for two cases: 1) the homoscedastic
case, and 2) the heteroscedastic case.
- d.
- Justify your answer in part b above by showing that in
the homoscedastic case your
choice of
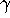 results in an IV estimator that has the smallest
asymptotic covariance matrix among all IV estimators.
results in an IV estimator that has the smallest
asymptotic covariance matrix among all IV estimators.
Question 1. (100 points) Consider the vector of observations contained in the file pop (populations in each of the 50 states, which
you also find in the  directory at the Statlab). Load it and call it X.
directory at the Statlab). Load it and call it X.
- a.
- Compute (X'R X)/49, where R is given
by
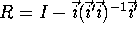 whre I is the
whre I is the
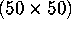 identity matrix and
identity matrix and  is a
is a 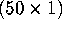 vector of ones. Could (X'RX)/49 ever be negative? Why or why not?
vector of ones. Could (X'RX)/49 ever be negative? Why or why not?
- b.
- Compute the sample standard deviation of the population of the
U.S. and the sample variance by using simple Gauss
commands.
- c.
- Compare your result in a. with your result in b.
Are the answers to a. and b. the same or different?
If they are the same, provide an explanation for why this is
the case.
(HINT:
you might want to examine X'RX. Recall the properties of the
matrix R, namely R= R'R = R*R, and see what R does to X).
Question 2 (100 points). Consider the set of hypothetical data on the regress model below.
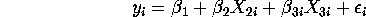
where
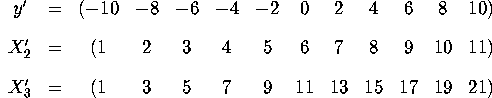
- a.
- Can you compute OLS estimates of the three unknowns
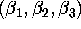 ?
?
- b.
- Is there a problem of multicollinearity in this
regression? If not, show that the columns of the X matrix
are linearly independent. If so, show that the columns of the
X matrix are linearly dependent.
- c.
- Throwing out any redundant columns of the
X matrix if necessary, what is the
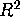 of the regression?
of the regression?
- d.
- Suppose that there are two students in the econ 551 class, whose names
are Jim and Tom. Suppose further that they estimated the parameters
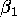 ,
, 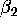 and
and 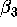 by trial and error. As a result,
however, Tom and Jim got different answers, i.e., (-6,-10,6) and (-10,-2,2), respectively. And each of them argues that his answer is
correct. What do you think about these two answers? Which answer fits better
to the data (in the sense of having
a higher
by trial and error. As a result,
however, Tom and Jim got different answers, i.e., (-6,-10,6) and (-10,-2,2), respectively. And each of them argues that his answer is
correct. What do you think about these two answers? Which answer fits better
to the data (in the sense of having
a higher 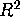 )?
)?
Question 3. (200 points)
One researcher wants to estimate the money demand equation by the
following regression:
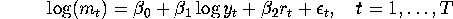
where: 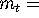 real money balances (i.e., nominal money balance deflated by the
price level),
real money balances (i.e., nominal money balance deflated by the
price level), 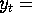 real GNP(i.e., nominal GNP deflated by the price level)
and
real GNP(i.e., nominal GNP deflated by the price level)
and 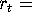 nominal interest rates.
nominal interest rates.
- a.
- What signs of the
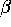 's do you expect from the economic theory? Explain why.
's do you expect from the economic theory? Explain why.
- b.
- Run the above regression using data files
accessible via anonymous ftp from gemini.econ.yale.edu
in the subdirectory
pub/John_Rust/courses/econ161/stats/timedat/fmt
or in the i:
 Spring99
Spring99  econ161
econ161  timedat
timedat  fmt directory at Statlab. You will be using the following variables:
GNP=Nominal GNP,
CPI=Price level,
R_3MO=Interest rates,
and
M2=Nominal money balances.
What is your estimates of
fmt directory at Statlab. You will be using the following variables:
GNP=Nominal GNP,
CPI=Price level,
R_3MO=Interest rates,
and
M2=Nominal money balances.
What is your estimates of 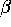 's ? On the basis of this evidence, what
do you conclude about the validity of the money demand equation given above?
's ? On the basis of this evidence, what
do you conclude about the validity of the money demand equation given above?
- c.
- Now another researcher is estimating somewhat different version of money
demand equation given by
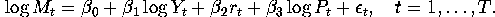
where 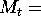 nominal money balances,
nominal money balances, 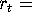 nominal interest rate,
nominal interest rate,
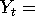 nominal GNP, and
nominal GNP, and  price level.
What signs of
price level.
What signs of 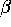 's do you expect? Why?
's do you expect? Why?
- d.
- Run the regression in part c using the data files given in b. What is your
estimates of
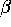 's ? On the basis of this evidence, what do you
conclude about the validity of the money demand equation given above?
's ? On the basis of this evidence, what do you
conclude about the validity of the money demand equation given above?
- e.
- Compare the two regression models in terms of
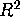 and/or the
plausibility of the estimated coefficients.
and/or the
plausibility of the estimated coefficients.
- f.
- Run a simple regression of aggregate consumption,
C on a
constant and
GNP.
What is your estimate of the marginal propensity
to consume.?
- g.
- Using the residuals calculated from your regression
in part f above, compute the serial correlation coefficient
of the regression residuals (i.e. compute
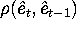 ). Are the residuals serially uncorrelated,
or negatively or positively correlated? Does your finding contradict the
normal equations that show that the residuals in a regression should be
``unpredictable'' in the sense of being uncorrelated with the
independent variables in the regression?
). Are the residuals serially uncorrelated,
or negatively or positively correlated? Does your finding contradict the
normal equations that show that the residuals in a regression should be
``unpredictable'' in the sense of being uncorrelated with the
independent variables in the regression?
Question 4 (200 points) Due to the fact that a large number
of buyers and sellers interact in a market for
a nearly homogeneous good, the market for soybeans is nearly perfectly
competitive. Contracts for soybeans on the Chicago Board
of Trade and the daily market or equilibrium price of soybeans is known
as the spot price. Demand for soybeans is a function of the
price of soybeans, p and personal income, y. Assume that the
aggregate demand curve for soybeans is linear:
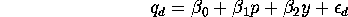
where 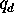 is the quantity of soybeans demanded,
p is the market price of soybeans, y is per capita
income and
is the quantity of soybeans demanded,
p is the market price of soybeans, y is per capita
income and 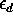 represents other unobserved factors affecting the demand for soybeans.
Assume the supply of soybeans
represents other unobserved factors affecting the demand for soybeans.
Assume the supply of soybeans 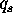 is also a linear function
of price, average rainfall r, and other factors
is also a linear function
of price, average rainfall r, and other factors 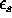 :
:
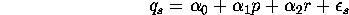
- a.
- What does economic theory (or common sense)
tell us about the signs of
the coefficients
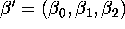 of the demand curve?
That is, do we expect the
of the demand curve?
That is, do we expect the 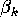 coefficients to be negative
positive or zero? (Explain your reasoning for full credit).
coefficients to be negative
positive or zero? (Explain your reasoning for full credit).
- b.
- What does economic theory (or common sense)
tell us about the signs of
the coefficients
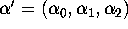 of the supply curve?
That is, do we expect the
of the supply curve?
That is, do we expect the 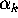 coefficients to be negative
positive or zero? (Explain your reasoning for full credit).
coefficients to be negative
positive or zero? (Explain your reasoning for full credit).
- c.
- The file
soy.asc
available via anonymous ftp at
gemini.econ.yale.edu in the subdirectory
pub/John_Rust/courses/econ161/soy.asc (the easiest way to get the
data is simply to click on the
gemini.econ.yale.edu in the subdirectory
soy.asc hyperlink on the
version of this problem set on the Econ 551 web page).
This data set
contains 200 monthly observations of soybean market prices, quantities
traded, per capita income y, and average rainfall, r. Retrieve these
data and estimate the parameters
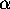 and
and 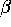 by running
OLS on the demand and supply side equation separately. Report
standard errors.
by running
OLS on the demand and supply side equation separately. Report
standard errors.
- d.
- Do the results from OLS confirm or disconfirm the hypotheses
you have made in part a and b? Explain why you are not getting the
expected results.
- e.
- Propose an estimator other than OLS that can improve your
results. Explain the theory behind the improvement.
- f.
- Provide estimates and standard errors of estimates using the
method proposed in part e.
State clearly how the method proposed in part e is implemented
for this particular problem, and with this particular data.
Summarize your
estimation results. Do the new results confirm the hypotheses?



Next: About this document
econ551
Mon Feb 22 15:32:01 EST 1999
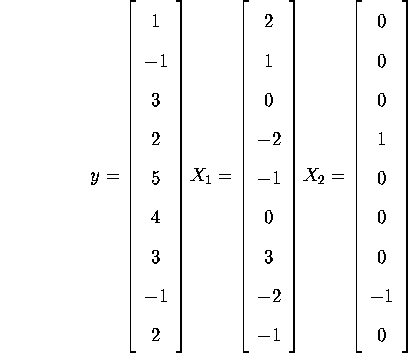
![]() /
/ ![]() , and
, and
![]() /
/ ![]() .
.
![]() and
and ![]() and compare them with those obtained in b.
and compare them with those obtained in b.
![]()
![]()
![]() is just the mean of y over the subpopulation
of individuals i with
is just the mean of y over the subpopulation
of individuals i with ![]() .
.
![]() /
/ ![]() , and
, and
![]() /
/ ![]() .
.
![]() and
and ![]() and compare them with those obtained in b.
and compare them with those obtained in b.
![]()
![]()
![]() is just the mean of y over the subpopulation
of individuals i with
is just the mean of y over the subpopulation
of individuals i with ![]() .
.
![]()
![]()

![]()
![]() , X is
, X is ![]() and
and ![]() is
an
is
an ![]() vector of error terms.
vector of error terms.
![]() matrix
of instruments and an
matrix
of instruments and an ![]() matrix of endogenous
regressors we form the instrumental variables estimator.
matrix of endogenous
regressors we form the instrumental variables estimator.
![]() directory at the Statlab). Load it and call it X.
directory at the Statlab). Load it and call it X.
![]()
![]()
![]() real money balances (i.e., nominal money balance deflated by the
price level),
real money balances (i.e., nominal money balance deflated by the
price level), ![]() real GNP(i.e., nominal GNP deflated by the price level)
and
real GNP(i.e., nominal GNP deflated by the price level)
and ![]() nominal interest rates.
nominal interest rates.
![]()
![]() nominal money balances,
nominal money balances, ![]() nominal interest rate,
nominal interest rate,
![]() nominal GNP, and
nominal GNP, and ![]() price level.
What signs of
price level.
What signs of ![]() 's do you expect? Why?
's do you expect? Why?
![]()
![]() is the quantity of soybeans demanded,
p is the market price of soybeans, y is per capita
income and
is the quantity of soybeans demanded,
p is the market price of soybeans, y is per capita
income and ![]() represents other unobserved factors affecting the demand for soybeans.
Assume the supply of soybeans
represents other unobserved factors affecting the demand for soybeans.
Assume the supply of soybeans ![]() is also a linear function
of price, average rainfall r, and other factors
is also a linear function
of price, average rainfall r, and other factors ![]() :
:
![]()