


Next: About this document ...
Spring 2001 John Rust
Economics 551b 37 Hillhouse, Rm. 27
PROBLEM SET 1
Regression Basics
QUESTION 1 This question is designed to help
you get a better appreciation for what
the ``Projection Theorem'' is and how it relates
to doing regression in practical situations.
- 1.
- Let P(y|X) denote the projection of
the vector y onto the subspace X. Define formally
what P(y|X) is.
- 2.
- State the Projection Theorem and give a geometrical
interpretation of the ``orthogonality'' between the projection
residual
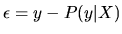 and the subspace X onto which
y is being projected.
and the subspace X onto which
y is being projected.
- 3.
- If
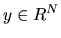 and
X is the subspace spanned by the
and
X is the subspace spanned by the
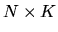 matrix of
regressors (which I also denote by X) in a regression, show
that
matrix of
regressors (which I also denote by X) in a regression, show
that
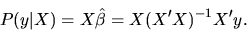 |
(1) |
- 4.
- Verify by a direct calculation that
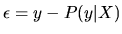 is orthogonal to X for the closed
form expression for P(y|X) given above.
is orthogonal to X for the closed
form expression for P(y|X) given above.
- 5.
- Prove that the projection operator satisfies:
|
P(P(y|X)|X) = P(y|X).
|
(2) |
Interpret this condition geometrically, and relate it to the
property of idempotence of the projection matrix
X(X'X)-1 X'.
- 6.
- Prove the Law of Iterated Projections i.e.
if X and Z are subspaces of a Hilbert space H and
X is a subspace of Z, then for any
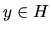 we have:
we have:
|
P(y|X) = P(P(y|Z)|X).
|
(3) |
- 7.
- Use the Law of Iterated Projections to show that
if you first regress y on the variables in the matrices
X and Z:
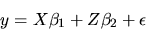 |
(4) |
and then you use the fitted
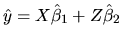 as
the dependent variable in the regression
as
the dependent variable in the regression
 |
(5) |
you will get the same numerical estimate of the estimated
regression coefficient
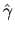 as if you regressed y on
X
as if you regressed y on
X
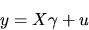 |
(6) |
However is it generally the case that
 ?
If so, provide a proof, if not, provide a counterexample
where
?
If so, provide a proof, if not, provide a counterexample
where
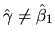 ?
?
- 8.
- Can you state conditions under which you can guarantee
that
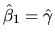 in the two regression in part
4 above?
in the two regression in part
4 above?
- 9.
- Let H be
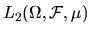 be the classical
L2 space, i.e. the space of all random variables defined on the
probability space
be the classical
L2 space, i.e. the space of all random variables defined on the
probability space
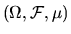 that have finite variance, with
inner product given by
that have finite variance, with
inner product given by
 |
(7) |
Let X denote the subspace spanned by the K random variables
 .
Find a formula for the projection
of the random variable
.
Find a formula for the projection
of the random variable 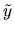 on X,
on X,
 ,
and provide
an interpretation of what it means.
,
and provide
an interpretation of what it means.
- 10.
- Let X be the space of all measurable functions of
the random variables
 that have
finite variance. Show that this is a subspace of
that have
finite variance. Show that this is a subspace of
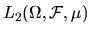 .
Given any
.
Given any
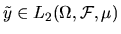 ,
what
is
,
what
is
 ?
?
- 11.
- If instead of
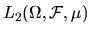 we consider
the space H=RN, and if X is the space of all measurable
functions of K vectors
we consider
the space H=RN, and if X is the space of all measurable
functions of K vectors
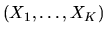 in RN, for
any
in RN, for
any 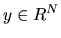 what is P(y|X)?
what is P(y|X)?
QUESTION 2
Consider the ``textbook'' regression model:
where X is regarded as a fixed (non-random)
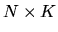 matrix and
the error vector
matrix and
the error vector 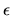 is a random vector with a
is a random vector with a
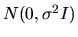 distribution, where
distribution, where
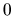 is
an
is
an
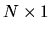 vector of 0's and
vector of 0's and
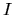 is an
is an
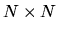 identity matrix, and
identity matrix, and
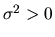 is a constant.
is a constant.
- 1.
- Show that OLS is a linear estimator of
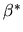 .
.
- 2.
- Show that an arbitrary linear estimator of
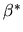 must
have the form M y for some matrix M. What are the dimensions
of M?
must
have the form M y for some matrix M. What are the dimensions
of M?
- 3.
- What constraints must be placed on M to result in an
unbiased estimator of
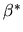 ?
?
- 4.
- What is the matrix M for the OLS estimator? Show that
for this choice of M the unbiasedness constraint that you derived
above is satisfied.
- 5.
- Show that the variance-covariance matrix for a linear
estimator of
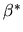 is given by
is given by
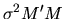 .
Does this formula
depend on M satisfying the restriction for unbiasedness, or will
it hold even for unbiased estimators of
.
Does this formula
depend on M satisfying the restriction for unbiasedness, or will
it hold even for unbiased estimators of 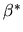 ?
?
- 6.
- Derive the covariance matrix for
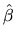 ,
the OLS
estimator.
,
the OLS
estimator.
- 7.
- Prove the Gauss Markov Theorem, i.e. show that the
OLS estimator is the best, linear, unbiased estimator of
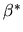 .
Hint: for an alternative estimator of the form
.
Hint: for an alternative estimator of the form
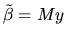 for some matrix M, write M as
for some matrix M, write M as
for some matrix C. Figure out what restrictions C needs to
satisfy so that
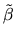 is an unbiased estimator, and then
use this to compute the covariance matrix for
is an unbiased estimator, and then
use this to compute the covariance matrix for
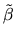 and show
that this exceeds the covariance matrix for
and show
that this exceeds the covariance matrix for 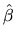 by a positive
semi-definite matrix.
by a positive
semi-definite matrix.



Next: About this document ...
John Rust
2001-01-31